Question

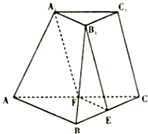
20．如图所示，在上、下底面对应边的比为1：2的三棱台中，过上底面一边A₁B₁作一个平行于棱C₁C的平面A₁B₁EF，则这个平面分三棱台成两部分的体积之比为（　　）

• A． 2：1
• B． 3：1
• C． 3：2
• D． 3：4

Answer 1

分析 利用三棱台的体积计算公式即可得出．

解答 解：设三棱台的高为h，上底的面积是S，则下底的面积是4S，
∴${V_{{A_1}{B_1}{C_1}-ABC}}=\frac{1}{3}h（S+4S+2S）=\frac{7}{3}Sh$，
∴${V_{棱柱{A_1}{B_1}{C_1}-EFC}}=Sh$，
∴$\frac{{{V_{棱柱{A_1}{B_1}{C_1}-EFC}}}}{{{V_台}-{V_{棱柱{A_1}{B_1}{C_1}-EFC}}}}=\frac{Sh}{{\frac{7}{3}Sh-Sh}}=\frac{3}{4}$．

点评 本题考查了三棱台的体积计算公式，考查了推理能力与计算能力，属于中档题．