
分析 (1)c2n+1-c2n-1=8;c2n+2-c2n=8.即可得出准等差数列{cn}的公差及其数列{cn}的前19项的和T19.
(2)①对于n∈N*,都有an+an+1=2n,an+1+an+2=2(n+1),可得:an+2-an=2.可得{an}为准等差数列,其公差为2.对n分类讨论,利用等差数列的通项公式即可得出.
②对n分类讨论,利用等差数列的通项公式与求和公式即可得出.
解答 (1)解:c2n+1-c2n-1=4×(2n-1)-1-[4×(2n-1)-1]=8;c2n+2-c2n=4×(2n+2)+9-(4×2n+9)=8.
∴准等差数列{cn}的公差为8,
{cn}的前19项的和T19=$\frac{(3+75)}{2}×10$+$\frac{(17+81)×9}{2}$=831.
(2)①证明:∵对于n∈N*,都有an+an+1=2n,an+1+an+2=2(n+1),∴an+2-an=2.
∴{an}为准等差数列,其公差为2.
当n为偶数时,an=2-a+2×$(\frac{n}{2}-1)$=n-a.
当n为奇数时,an=a+2×$(\frac{n+1}{2}-1)$=n+a-1.
∴an=$\left\{\begin{array}{l}{n+a-1,n为奇数}\\{n-a,n为偶数}\end{array}\right.$.
②当n为偶数时,Sn=$a×\frac{n}{2}$+$\frac{\frac{n}{2}(\frac{n}{2}-1)}{2}×2$+$(2-a)×\frac{n}{2}$+$\frac{\frac{n}{2}(\frac{n}{2}-1)}{2}×2$=$\frac{1}{2}{n}^{2}$.
当n为奇数时,Sn=$a×\frac{n+1}{2}$+$\frac{\frac{n+1}{2}(\frac{n+1}{2}-1)}{2}$×2+(2-a)×$\frac{n-1}{2}$+$\frac{\frac{n-1}{2}(\frac{n-1}{2}-1)}{2}×2$=$\frac{1}{2}{n}^{2}$+a-$\frac{1}{2}$.
当k为偶数时,Sk=$\frac{1}{2}{k}^{2}$=50,解得k=10.
S9=$\frac{1}{2}×{9}^{2}$+a-$\frac{1}{2}$=40+a=50,解得a=10.
S11=$\frac{1}{2}×1{1}^{2}$+a-$\frac{1}{2}$=50,解得a=-10.
∴存在实数a=±10,使得数列{Sn}有连续的两项都等于50.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式、新定义,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | x-y-4=0 | C. | x+y-2=0 | D. | x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
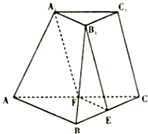 如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边A1B1作一个平行于棱C1C的平面A1B1EF,则这个平面分三棱台成两部分的体积之比为( )
如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边A1B1作一个平行于棱C1C的平面A1B1EF,则这个平面分三棱台成两部分的体积之比为( )| A. | 2:1 | B. | 3:1 | C. | 3:2 | D. | 3:4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com