
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据指数函数,对数函数的性质,利用充分条件和必要条件的定义进行判断即可.
解答 解:若“($\frac{1}{2}$)a<($\frac{1}{2}$)b”,则根据指数函数的单调性的性质可知a>b,
当a,b由负值或等于0时,log2a>log2b不成立,不是充分条件,
若log2a>log2b,则a>b>0.此时“($\frac{1}{2}$)a<($\frac{1}{2}$)b”成立,是必要条件,
∴“($\frac{1}{2}$)a<($\frac{1}{2}$)b”是“log2a>log2b”的必要不充分条件;
故选:B.
点评 本题主要考查充分条件和必要条件的应用,利用指数函数,对数函数的单调性是解决本题的关键,比较基础.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$<x<$\frac{1}{5}$ | B. | $\frac{1}{6}$<x<$\frac{1}{5}$ | C. | $\frac{1}{12}$<x<$\frac{2}{3}$ | D. | $\frac{1}{6}$<x<$\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{3}}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
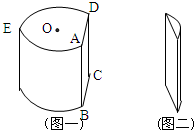 如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.
如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 随机数表法 | C. | 系统抽样法 | D. | 分层抽样法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com