
分析 (1)求导函数,利用直线y=2x+m与函数y=f(x)的图象相切,求切点坐标,即可求m的值;
(2)利用f(x)在[1,2]上是单调减函数,可得f′(x)=lnx+1-$\frac{a}{x}$,≤0在[1,2]上恒成立,分离参数,求最值,即可求得a的最小值;
解答 解:(1)当a=0时,f(x)=xlnx,
∴f′(x)=lnx+1,
∵直线y=2x+m与函数y=f(x)的图象相切,
∴斜率k=f′(x)=lnx+1=2,解得:x=2
∵f(e)=e,
∴切点为(e,e),
∴m=-e;
(2)∵f(x)=(x-a)lnx,求导,f′(x)=lnx+1-$\frac{a}{x}$,
∵f(x)在[1,2]上是单调减函数,
∴f′(x)=lnx+1-$\frac{a}{x}$≤0在[1,2]上恒成立
∴a≥xlnx+x在[1,2]上恒成立
令g(x)=xlnx+x,则g′(x)=lnx+2>0
∴g(x)=xlnx+x在[1,2]上单调递增
∴a≥g(2)=2ln2+2
∴a的最小值为2ln2+2;
点评 本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,考查分离参数求最值的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | x-y-4=0 | C. | x+y-2=0 | D. | x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
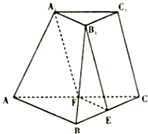 如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边A1B1作一个平行于棱C1C的平面A1B1EF,则这个平面分三棱台成两部分的体积之比为( )
如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边A1B1作一个平行于棱C1C的平面A1B1EF,则这个平面分三棱台成两部分的体积之比为( )| A. | 2:1 | B. | 3:1 | C. | 3:2 | D. | 3:4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com