
分析 把AB长度调整,两个极端分别为C,D重合,A,D重合分别计算两种极限前提下AB的长度,利用割补法求出四边形ABCD面积的取值范围.
解答 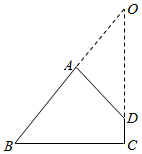 解:平面四边形ABCD中,∠A=∠B=60°,∠D=150°,∴∠C=90°.
解:平面四边形ABCD中,∠A=∠B=60°,∠D=150°,∴∠C=90°.
当把AB长度调整,两个极端分别为C,D重合时,AB=BC=1;
当A,D重合时,由正弦定理得$\frac{1}{sin30°}$=$\frac{AB}{sin90°}$,解得AB=2;
故AB的取值范围是(1,2),
设AD=x,则AO=x,∠OAD=120°四边形ABCD面积S=$\frac{1}{2}×1×\sqrt{3}$-$\frac{1}{2}{x}^{2}×sin120°$=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{4}{x}^{2}$,
∵OB=2,∴x∈(0,1),∴S∈($\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{2}$).
故答案为:($\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了正弦定理的运用以及极限思想;关键是把AB长度调整,两个极端分别为C.D重合,A,D重合.


科目:高中数学 来源: 题型:解答题
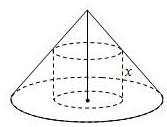 如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.
如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1] | B. | [-2,-1] | C. | (-∞,-1]∪[0,+∞) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P-ABC的正视图与俯视图的面积之比的最大值为( )
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P-ABC的正视图与俯视图的面积之比的最大值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com