
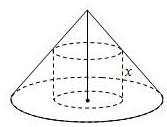
 如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.
如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.分析 (1)设圆柱的底面半径为r,根据相似比求出r与x的关系,代入侧面积公式即可;
(2)利用二次函数的性质求出侧面积最大时x的值,代入体积公式即可.
解答 解:(1)设圆柱的半径为r,则$\frac{r}{2}=\frac{2-x}{2}$,∴r=2-x,0<x<2.
∴S圆柱侧=2πrx=2π(2-x)x=-2πx2+4πx.(0<x<2).
(2)${S_{圆柱侧}}=2π(2x-{x^2})=2π[-{(x-1)^2}+1]$,
∴当x=1时,S圆柱侧取最大值2π,
此时,r=1,所以${V_{圆柱}}=π{r^2}x=π$.
点评 本题考查了旋转体的结构特征,体积计算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com