
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() 是边长为2 的正三角形,
是边长为2 的正三角形, ![]() .
.
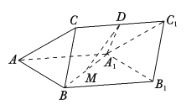
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)取AB的中点H,连接HM,CH,证明四边形CDMH是平行四边形得出DM∥CH,从而有DM∥平面ABC;
(2)取BB1中点E,以E为原点建立坐标系,求出两半平面的法向量,计算法向量的夹角即可得出二面角的大小.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
∴![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
则四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,∵
,∵![]() 为等边三角形, ∴
为等边三角形, ∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
建立以![]() 为坐标原点,
为坐标原点, ![]() 分别为
分别为![]() 轴的空间直角坐标系如图:
轴的空间直角坐标系如图:
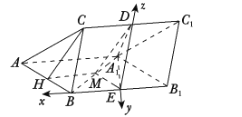
则![]()
![]() ,
, ![]() ,
,
则设平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,即
,即
令![]() ,则
,则![]() ,即
,即![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
, ![]() ,
,
则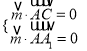 ,得
,得 ,即
,即 ,
,
令![]() ,则
,则![]() ,即
,即![]() ,
,
则![]()

![]() ,
,
即二面角![]() 的余弦值是
的余弦值是![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上动点,点
是圆上动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]()
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,与(1)中所求点
相切,与(1)中所求点![]() 的轨迹教育不同的两点
的轨迹教育不同的两点![]()
![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设 ![]() =x
=x ![]() ,
, ![]() ,记y=f(x).
,记y=f(x).
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,x∈[0,1].若对任意x1∈[ ![]() ,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象部门预报,在距离码头A南偏东45°方向400千米B处的台风中心正以20千米每小时的速度向北偏东15°方向沿直线移动,以台风中心为圆心,距台风中心100 ![]() 千米以内的地区都将受到台风影响.据以上预报估计,从现在起多长时间后,码头A将受到台风的影响?影响时间大约有多长?
千米以内的地区都将受到台风影响.据以上预报估计,从现在起多长时间后,码头A将受到台风的影响?影响时间大约有多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() .若
.若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及样本频率分布表如下:
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | ② |
[80,90) | ① | 0.24 |
[90,100] | 4 | 0.08 |
合计 | ③ | ④ |
(1)请把给出的样本频率分布表中的空格都填上;
(2)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,且a1+3,3a2 , a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)求数列{an+log2an}(n∈N*)的前10项和T10 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com