Question

【题目】如图，D是AC的中点，四边形BDEF是菱形，平面平面ABC，，，．

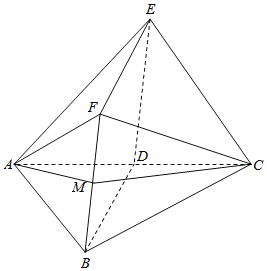
若点M是线段BF的中点，证明：平面AMC；

求平面AEF与平面BCF所成的锐二面角的余弦值．

Answer 1

【答案】（1）见解析；（2）.

【解析】

试题分析：（1）连接，. .由四边形为菱形，可证.由平面平面，可证平面.即可证明平面；

2）设线段的中点为，连接.易证平面.以为坐标原点，，，所在直线分别为轴，轴，轴建立如图所示的空间直角坐标系.求出相应点及向量的坐标，求得平面，平面的法向量，.。利用空间向量夹角公式可求得平面与平面所成的锐二面角的余弦值.

试题解析：

（1）连接，∵四边形为菱形，且，

∴为等边三角形.

∵为的中点，∴.

∵，，又是的中点，

∴.

∵平面平面，平面平面，平面，

∴平面.

又平面，∴.

由，，，

∴平面.

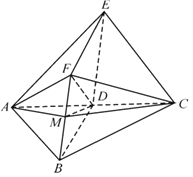
（2）设线段的中点为，连接.易证平面.以为坐标原点，，，所在直线分别为轴，轴，轴建立如图所示的空间直角坐标系.则，，，，.

∴，，，.

设平面，平面的法向量分别为，.

由 .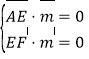

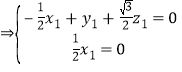解得.

取，∴.

又由 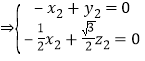解得.

取，∴.

∵ .

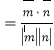
∴平面与平面所成的锐二面角的余弦值为.