
【题目】已知函数f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1时,求方程f(x)=g(x)的实根;
(2)若对任意的x∈(1,+∞),函数y=g(x)的图象总在函数y=f(x)图象的上方,求m的取值范围;
(3)求证: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
【答案】(1)见解析(2) ![]() .(3) 见解析
.(3) 见解析
【解析】试题分析:(1)代入![]() 时,
时, ![]() ,即
,即![]() ,整理方程得
,整理方程得![]() ,利用导数判断函数的单调性为递减函数,故最多有一个零点,而
,利用导数判断函数的单调性为递减函数,故最多有一个零点,而![]() ,故方程
,故方程![]() 有唯一的实根
有唯一的实根![]() ;(2)对于任意的
;(2)对于任意的![]() ,
, ![]() 恒成立,通过构造函数
恒成立,通过构造函数![]() ,利用导函数判断函数的单调性,
,利用导函数判断函数的单调性, ![]() ,通过讨论
,通过讨论![]() ,判断是否符合题意;(3)由(2)知,当
,判断是否符合题意;(3)由(2)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立,结合题型,构造不妨令
成立,结合题型,构造不妨令![]() ,得出
,得出![]() ,利用累加可得结论.
,利用累加可得结论.
试题解析:(1) ![]() 时,
时, ![]() ,即
,即![]() ,而
,而![]() ,所以方程即为
,所以方程即为![]() .
.
令![]() ,则
,则![]() ,而
,而![]() ,故方程
,故方程![]() 有唯一的实根
有唯一的实根![]() .
.
(2)对于任意的![]() ,函数
,函数![]() 的图象总在函数
的图象总在函数![]() 图象的上方,
图象的上方,
即![]() ,
, ![]() ,即
,即![]() ,
,
设![]() ,即
,即![]() ,
, ![]() ,则
,则![]()
①若![]() ,则
,则![]() ,
, ![]() ,这与题设
,这与题设![]() 矛盾.
矛盾.
若![]() ,方程
,方程![]() 的判别式
的判别式![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即不等式成立.
,即不等式成立.
当![]() ,即
,即![]() 时,方程
时,方程![]() 有两个实根,设两根为
有两个实根,设两根为![]() ,
, ![]() 且
且![]() ,则
,则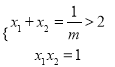
∴方程有两个正实根且![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增, ![]() 与题设矛盾.
与题设矛盾.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(3)证明 由(2)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立.
成立.
不妨令![]()
∴![]() ,即
,即
![]()
∴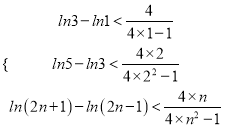 ,累加可得
,累加可得![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
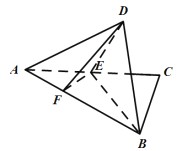
(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为![]() |OB|.
|OB|.
(1)求椭圆C的方程;
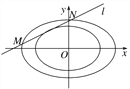
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() ,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
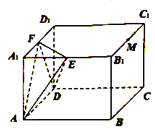
(1)在图中画出这个几何图形(说明画法,不需要说明理由);
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金砖国家领导人第九次会晤于2017年9月3日至5日在中国福建厦门市举行,为了在金砖峰会期间为来到厦门的外国嘉宾提供服务,培训部对两千余名志愿者进行了集中培训,为了检验培训效果,现培训部从两千余名志愿者中随机抽取100名,按年龄(单位:岁)分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者前去机场参加接待外宾礼仪测试,则应从第3,4,5组中各抽取多少名志愿者?
(2)在(1)的条件下,若在第3,4组的志愿者中随机抽取2名志愿者介绍接待外宾经验感受,求第4组至少有1名志愿者被抽中的概率.
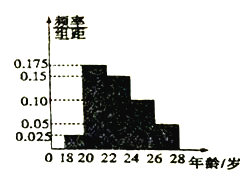
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,离心率是
,离心率是![]() ,直线
,直线![]() 过点
过点![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,
时, ![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当直线![]() 绕点
绕点![]() 运动时,试求
运动时,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com