Question

6．在平面区域{（x，y）|0≤x≤1，1≤y≤2}内随机投入一点P，则点P的坐标（x，y）满足y≤2x的概率为（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{2}$
• C． $\frac{2}{3}$
• D． $\frac{3}{4}$

Answer 1

分析 作出不等式组对应的区域，利用几何概型的概率公式，即可得到结论．

解答 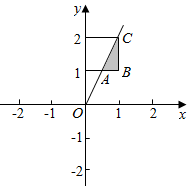解：不等式组$\left\{\begin{array}{l}{0≤x≤1}\\{1≤y≤2}\end{array}\right.$表示的平面区域为D的面积为1，
不等式y≤2x对应的区域为三角形ABC，
则三角形ABC的面积S=$\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$，
则在区域D内任取一点P（x，y），则点P满足y≤2x的概率为$\frac{1}{4}$，
故选：A．

点评 本题主要考查二元一次不等式表示平面区域以及几何概型的概率计算，利用条件求出对应区域的面积是解决本题的关键．