
����Ŀ���¹ڷ��������ڼ䣬Ϊȷ����ͣ�β�ͣѧ������У������֯�����Ͻ�ѧ�����ѧ��ijУ���÷ֲ�����ķ����������꼶��ѧ���г�ȡһ������Ϊ150���������й������Ͻ�ѧʵʩ������ʾ����飮��֪��У��һ�꼶����ѧ��660�ˣ���ȡ�������и߶��꼶��50�ˣ������꼶��45�ˣ��±��Ǹ��ݳ�����������õ��ĸ߶�ѧ����˯��ʱ�䣨��λ��h����Ƶ�ʷֲ�����
���� | Ƶ�� | Ƶ�� |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
�ϼ� | 50 | 1 |
��1�����Уѧ��������
��2����Ƶ�ʷֲ�����ʵ��x��y��z��ֵ��
��3����֪��˯��ʱ��������[6��6.5)��5���߶�ѧ���У���2��Ů����3����������������ѡ2�˽�����̸����ѡ�е�2��ǡ��Ϊһ��һŮ�ĸ��ʣ�
���𰸡���1��1800�ˣ���2��7,0.24,8����3��![]() .
.
��������
��1�����ݸ�һ�꼶ѧ���������г�������⣻��2������Ƶ�ʡ�Ƶ���������Ĺ�ϵ���㣻��3���оٳ�5���߶�ѧ������ѡ2�˵����п��ܽ������ȷ��2����ǡ��Ϊһ��һŮ�Ŀ��ܣ����ùŵ�����ʹ�ʽ�������.
��1�����Уѧ������Ϊn��
������![]() �����n��1800��
�����n��1800��
���Ը�Уѧ������Ϊ1800�ˣ�
��2��������![]() �����x��7��
�����x��7��![]() ��
��
![]() .
.
��3������ѡ�е�2��ǡ��Ϊһ��һŮ��Ϊ�¼�A��
��5���߶�ѧ����Ů��ΪF1��F2������ΪM1��M2��M3��
������ѡ2�������������(F1��F2)��(F1��M1)��(F1��M2)��(F1��M3)��(F2��M1)��(F2��M2)��(F2��M3)��(M1��M2)��(M1��M3)��(M2��M3)��
�����¼�����10���������ǵȿ��ܵģ�
�¼�A�����Ļ����¼���6������P(A)��![]() ��
��![]() ��
��
����ѡ�е�2��ǡ��Ϊһ��һŮ�ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ae2x+(a��2) ex��x.
ae2x+(a��2) ex��x.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ��������㣬��a��ȡֵ��Χ.
��������㣬��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() �͵�
�͵�![]() .
.
��1������![]() ��Բ
��Բ![]() �����ߣ������ߵķ��̣�
�����ߣ������ߵķ��̣�
��2�����Ե�![]() ΪԲ�ģ��ұ�ֱ��
ΪԲ�ģ��ұ�ֱ��![]() �صõ��ҳ�Ϊ8��Բ
�صõ��ҳ�Ϊ8��Բ![]() �ķ��̣�
�ķ��̣�
��3����![]() Ϊ��2����Բ
Ϊ��2����Բ![]() ������һ�㣬����
������һ�㣬����![]() ��Բ
��Բ![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ����̽����ƽ�����Ƿ����һ����
����̽����ƽ�����Ƿ����һ����![]() ��ʹ��
��ʹ��![]() Ϊ��ֵ�������ڣ����������
Ϊ��ֵ�������ڣ����������![]() �����꣬��ָ����Ӧ�Ķ�ֵ���������ڣ���˵������.
�����꣬��ָ����Ӧ�Ķ�ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABC-A1B1C1�У������ABC��ֱ�������Σ�AC=BC=AA1=2��DΪ����AA1���е㣮

��1��������ֱ��DC1��B1C���ɽǵ�����ֵ��
��2��������B1-DC-C1��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() �� ����
�� ����![]() ����,
����, ![]() ��
��![]() .
.
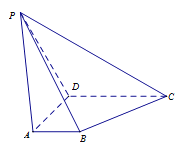
������֤��![]() ƽ��
ƽ��![]() ��
��
������֤��![]() ƽ��
ƽ��![]() ��
��
������![]() ����
����![]() ���е㣬��֤��������
���е㣬��֤��������![]() ������һ��
������һ��![]() ��
��![]() ��
��![]() ����ƽ��
����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��A(0����2)��B(4��0)��ԲC������(0����1)��(0��1)��(![]() ��0)��б��Ϊk��ֱ��l������B��
��0)��б��Ϊk��ֱ��l������B��
��1����ԲC�ı����̣�
��2����k��2ʱ����ֱ��l�ϵ�һ��P��ԲC��һ�����ߣ��е�ΪQ��������PQ��![]() �����P�����ꣻ
�����P�����ꣻ
��3����M��N��ԲC������������ͬ�ĵ㣬����MNΪֱ����Բ��ֱ��l��û�й����㣬��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�鷨��Ȥ����3����ͬѧA��B��C��3��ŮͬѧX��Y��Z�����꼶������±���
һ�꼶 | ���꼶 | ���꼶 | |
��ͬѧ | A | B | C |
Ůͬѧ | X | Y | Z |
�ִ���6��ͬѧ�����ѡ��2�˲μ��鷨����![]() ÿ�˱�ѡ���Ŀ�������ͬ
ÿ�˱�ѡ���Ŀ�������ͬ![]() ��
��
![]() �ñ�����ĸ�оٳ����п��ܵĽ����
�ñ�����ĸ�оٳ����п��ܵĽ����
![]() ��MΪ�¼���ѡ����2�����Բ�ͬ�꼶���Ա���ͬ�������¼�M�����ĸ��ʣ�
��MΪ�¼���ѡ����2�����Բ�ͬ�꼶���Ա���ͬ�������¼�M�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�����
�У�����![]() �����Σ���
��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
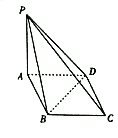
��1��֤����![]() ƽ��
ƽ��![]() .
.
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪������ϵ![]() ��ԭ��ͼ�����ϵ
��ԭ��ͼ�����ϵ![]() �ļ����غϣ�
�ļ����غϣ�![]() ��Ǹ������뼫���غϣ� ��λ������ͬ�� ��ֱ������ϵ�£� ����
��Ǹ������뼫���غϣ� ��λ������ͬ�� ��ֱ������ϵ�£� ����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������ ��
������ ��
��1�� д������![]() �ļ����귽�̣�
�ļ����귽�̣�
��2�� ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ��ƽ��ֱ������ϵ�еĽ������� ��
��ƽ��ֱ������ϵ�еĽ������� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com