Question

【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.

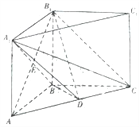
(1)求证：BD⊥A1C；

(2)求证：AB1⊥平面A1BC。

Answer 1

【答案】（1）见解析（2）见解析

【解析】试题分析：（1）先根据线面平行性质定理得B1C//ED，再根据等腰三角形性质得BD⊥AC，根据直棱柱性质得A1A⊥BD，最后根据线面垂直判定定理得结论，（2）根据菱形性质得AB1⊥A1B,再根据直棱柱性质得BC⊥BB1， 由AB⊥BC,根据线面垂直判定定理得BC⊥平面ABB1A.即得BC⊥AB1,最后根据线面垂直判定定理得结论.

试题解析：

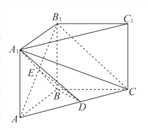
(I)证明:连结ED,∵平面AB1C平面A1BD=ED，B1C//平面A1BD,

∴B1C//ED,.

∵E为AB1中点,∴D为AC中点;..

∵∠BAC=∠BCA=∠ABC,∴AB=BC,∴BD⊥AC,.

由A1A⊥平面ABC,BD平面ABC,得A1A⊥BD.

由及A1A、AC是平面A1ACC1内的两条相交直线，

得BD⊥平面A1ACC1，

因为A1C平面AlACC1,故BD⊥A1C

(Ⅱ)由（Ⅰ）知AB=BC,AB⊥BC,.

∵BB1=BC，∴四边形ABB1A1是菱形，∴AB1⊥A1B,.

∵BB1⊥平面ABC,BC平面ABC.∴BC⊥BB1.

∵ABBB1=B,AB,BB1平面ABB1A1.∴BC⊥平面ABB1A..

∵AB1平面ABB1A1,∴BC⊥AB1,....

∵BCA1B=B,BC,A1B平面A1BC,∴AB1⊥平面A1BC.

点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.

(1)证明线面、面面平行，需转化为证明线线平行.

(2)证明线面垂直，需转化为证明线线垂直.

(3)证明线线垂直，需转化为证明线面垂直.