练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线E：的焦点为F，是抛物线E上一点，且．

    1求抛物线E的标准方程；

    2设点B是抛物线E上异于点A的任意一点，直线AB与直线交于点P，过点P作x轴的垂线交抛物线E于点M，设直线BM的方程为，k，b均为实数，请用k的代数式表示b，并说明直线BM过定点．

    【答案】（1）；（2）见解析

    【解析】

    1利用抛物线的定义与性质求p的值，即可写出抛物线方程；2设点，，由直线BM的方程和抛物线方程联立，消去y，利用根与系数的关系和A，P，B三点共线，化简整理可得BM的方程，从而求出直线BM所过的定点．

    解：1根据题意知，，①

    因为，所以，②

    联立①②解得，；

    所以抛物线E的标准方程为；

    2设，；

    又直线BM的方程为，代入，得；

    由根与系数的关系，得，；③

    由轴及点P在直线上，得，

    则由A，P，B三点共线，得，

    整理，得；

    将③代入上式并整理，得，

    由点B的任意性，得，即，

    所以；

    即直线BM恒过定点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.

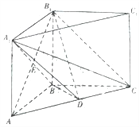
    (1)求证：BD⊥A1C；

    (2)求证：AB1⊥平面A1BC。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设关于某种设备的使用年限(年)与所支出的维修费用 (万元)有如下统计：

    2

    3

    4

    5

    6

    2.2

    3.8

    5.5

    6.5

    7.0

    已知， . ，

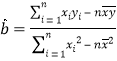    (1)求， ；

    (2)与具有线性相关关系，求出线性回归方程；

    (3)估计使用年限为10年时，维修费用约是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的部分图象如图所示.

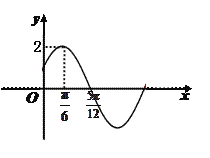
    （1） 求函数的解析式；

    （2） 如何由函数的通过适当图象的变换得到函数的图象， 写出变换过程;

    （3） 若，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆： 的左、右焦点、，其焦距为，点在椭圆的内部，点是椭圆上的动点，且恒成立，则椭圆离心率的取值范围是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】牡丹江一中2019年将实行新课程改革，即除语、数、外三科为必考科目外，还要在理、化、生、史、地、政六科中选择三科作为选考科目．已知某生的高考志愿为北京大学环境科学专业，按照17年北大高考招生选考科目要求物、化必选，为该生安排课表（上午四节、下午四节，上午第四节和下午第一节不算相邻），现该生某天最后两节为自习课，且数学不排下午第一节，语文、外语不相邻，则该生该天课表有（　　）种．

    A. 444B. 1776C. 1440D. 1560

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），其中.以原点为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求出曲线的普通方程和曲线的直角坐标方程；

    （2）已知曲线与交于， 两点，记点， 相应的参数分别为， ，当时，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍，再横坐标不变纵坐标伸长到原来的2倍，最后向右平移个单位而得到.

    ⑴求f(x)的解析式与最小正周期；

    ⑵求f(x)在x∈(0，π)上的值域与单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为 (为参数），以为极点， 轴的非负半轴为极轴的极坐标系中，直线的极坐标方程为.

    （1）求曲线的极坐标方程；

    （2）设直线与曲线相交于两点，求的值.

    【答案】（1）曲线的极坐标方程为： ；（2）6.

    【解析】试题分析：（1）先根据三角函数平方关系消参数得曲线的普通方程，再根据化为极坐标方程；（2）将直线l的极坐标方程代入曲线的极坐标方程得，再根据求的值．

    试题解析：解:（1）将方程消去参数得，

    ∴曲线的普通方程为，

    将代入上式可得，

    ∴曲线的极坐标方程为： ． -

    （2）设两点的极坐标方程分别为,

    由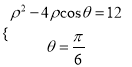消去得，

    根据题意可得是方程的两根，

    ∴，

    ∴．

    【题型】解答题
    【结束】
    23

    【题目】选修4—5：不等式选讲

    已知函数．

    (1)当时，求关于x的不等式的解集；

    (2)若关于x的不等式有解，求a的取值范围．

    查看答案和解析>>

    同步练习册答案