
分析 设点P(x,$\frac{1}{x}$)(x>0),利用两点间的距离公式可得|PA|,令t=x+$\frac{1}{x}$,由x>0,可得t≥2,令g(t)=t2-2at+2a2-2=(t-a)2+a2-2,讨论a的范围:当0<a≤2时,当a>2时,利用基本不等式和二次函数的单调性即可得出a的值.
解答 解:设点P(x,$\frac{1}{x}$)(x>0),
则|PA|=$\sqrt{(x-a)^{2}+(\frac{1}{x}-a)^{2}}$
=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2a(x+\frac{1}{x})+2{a}^{2}}$
=$\sqrt{(x+\frac{1}{x})^{2}-2a(x+\frac{1}{x})+2{a}^{2}-2}$,
令t=x+$\frac{1}{x}$,由x>0,可得t≥2,
令g(t)=t2-2at+2a2-2=(t-a)2+a2-2,
①当0<a≤2时,t=2时g(t)取得最小值g(2)=2-4a+2a2=(2 $\sqrt{2}$)2,
解得a=-1,3,均舍去;
②当a>2时,g(t)在区间[2,a)上单调递减,在(a,+∞)单调递增,
可得t=a,g(t)取得最小值g(a)=a2-2,可得a2-2=(2 $\sqrt{2}$)2,解得a=$\sqrt{10}$(负的舍去).
综上可知:a=$\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题综合考查了两点间的距离公式、基本不等式的性质、二次函数的单调性等基础知识和基本技能,考查了分类讨论的思想方法、推理能力和计算能力.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
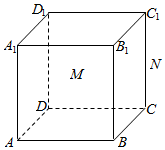 在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为A1B1,C1C的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为A1B1,C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com