
分析 如图所示,由$\overrightarrow{MN}$=$\overrightarrow{MB}$+$\overrightarrow{BN}$,且$\overrightarrow{BN}$=$\frac{1}{3}$$\overrightarrow{N{C}_{1}}$,可得$\overrightarrow{MB}$=$-\overrightarrow{BM}$=-$\frac{1}{2}$$(\overrightarrow{BA}+\overrightarrow{BC})$=-$\frac{1}{2}$$(-\overrightarrow{AB}+\overrightarrow{AD})$,$\overrightarrow{BN}$=$\frac{1}{4}$$\overrightarrow{B{C}_{1}}$=$\frac{1}{4}$$(\overrightarrow{BC}+\overrightarrow{B{B}_{1}})$=$\frac{1}{4}$$(\overrightarrow{AD}+\overrightarrow{A{A}_{1}})$,代入即可得出.
解答 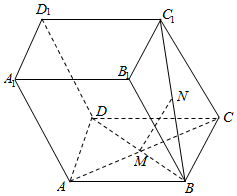 解:如图所示,
解:如图所示,
∵$\overrightarrow{MN}$=$\overrightarrow{MB}$+$\overrightarrow{BN}$,且$\overrightarrow{BN}$=$\frac{1}{3}$$\overrightarrow{N{C}_{1}}$,
$\overrightarrow{MB}$=$-\overrightarrow{BM}$=-$\frac{1}{2}$$(\overrightarrow{BA}+\overrightarrow{BC})$=-$\frac{1}{2}$$(-\overrightarrow{AB}+\overrightarrow{AD})$,
$\overrightarrow{BN}$=$\frac{1}{4}$$\overrightarrow{B{C}_{1}}$=$\frac{1}{4}$$(\overrightarrow{BC}+\overrightarrow{B{B}_{1}})$=$\frac{1}{4}$$(\overrightarrow{AD}+\overrightarrow{A{A}_{1}})$,
∴$\overrightarrow{MN}$=$\frac{1}{2}$$(\overrightarrow{AD}-\overrightarrow{AB})$+$\frac{1}{4}$$(\overrightarrow{AD}+\overrightarrow{A{A}_{1}})$
=$-\frac{1}{2}\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$+$\frac{1}{4}$$\overrightarrow{A{A}_{1}}$,
又$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{A{A}_{1}}$,
则α=-$\frac{1}{2}$,β=$\frac{3}{4}$,γ=$\frac{1}{4}$.
故答案为:-$\frac{1}{2}$,$\frac{3}{4}$,$\frac{1}{4}$.
点评 本题考查了向量共线定理、平面向量共线定理、空间向量基本定理,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
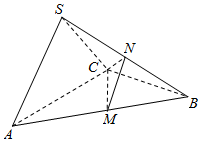 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
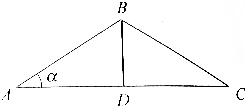 如图,屋顶的断面图是等腰三角形ABC,其中AB=BC,横梁AC的长为定值2l,试问:当屋顶面的倾斜角α为多大时,雨水从屋顶(顶面为光滑斜面)上流下所需A的时间最短?
如图,屋顶的断面图是等腰三角形ABC,其中AB=BC,横梁AC的长为定值2l,试问:当屋顶面的倾斜角α为多大时,雨水从屋顶(顶面为光滑斜面)上流下所需A的时间最短?查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{\sqrt{6}}}{32}π{a^3}$ | B. | $\frac{{\sqrt{6}}}{8}π{a^3}$ | C. | $\sqrt{6}π{a^3}$ | D. | $\frac{{\sqrt{6}}}{3}π{a^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com