考点:命题的真假判断与应用
专题:三角函数的图像与性质,简易逻辑
分析:①对k分类讨论可得:函数y=sin(kπ-x)=(-1)
k+1sinx(k∈Z)为奇函数;
②利用倍角公式可得:函数y=sin
4x-cos
4x=-cos2x,其最小正周期是π;
③由于
f(-)=
cos[2×(-)+]=cos(-π)=-1,可知函数
y=cos(2x+)的图象的一条对称轴为x=-
π;
④由
+2kπ≤x+≤+2kπ,解得
+4kπ≤x≤4kπ+(k∈Z).分别取k=-1,0即可得出函数
y=sin(x+)在[-2π,2π]上单调减区间.
解答:
解:①函数y=sin(kπ-x)=(-1)
k+1sinx(k∈Z)为奇函数,正确;
②函数y=sin
4x-cos
4x=-cos2x,其最小正周期是π,因此不正确;
③∵
f(-)=
cos[2×(-)+]=cos(-π)=-1,因此函数
y=cos(2x+)的图象的一条对称轴为x=-
π,正确;
④由
+2kπ≤x+≤+2kπ,解得
+4kπ≤x≤4kπ+(k∈Z).当k=-1时,函数f(x)的单调递减区间为
[-2π,-];当k=0时,函数f(x)的单调递减区间为
[,2π],可得函数
y=sin(x+)在[-2π,2π]上单调减区间是
[-2π,-],
[,2π].其次其单调区间不能用“∪”,因此不正确.
其中正确结论的序号为①③.
故答案为:①③.
点评:本题考查了三角函数的图象与性质、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.



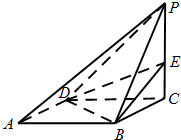 已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.
已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.