考点:命题的真假判断与应用
专题:
分析:A.“am2<bm2”⇒“a<b”,反之m=0不成立;
B.f′(x0)=0,则设函数f(x)在x=x0取得极值的必要非充分条件,例如f(x)=x3,虽然f′(0)=0,但是,0不是函数f(x)的极值点;
C.利用轴对称的性质即可判断出;
D.由于f(x+1)=-f(x),可得f(x+2)=-f(x+1)=f(x),可得周期T=2.
解答:
解:A.“am2<bm2”⇒“a<b”,反之m=0不成立,因此“am2<bm2”是“a<b”的充分不必要条件,正确;
B.f′(x0)=0,则设函数f(x)在x=x0取得极值的必要非充分条件,例如f(x)=x3,虽然f′(0)=0,但是,0不是函数f(x)的极值点,因此不正确;
C.函数y=f(x)满足f(x+1)=f(1-x),则其图象关于直线x=1对称,正确;
D.∵f(x+1)=-f(x),∴f(x+2)=-f(x+1)=f(x),∴周期T=2,正确.
综上可得:只有B错误.
故选:B.
点评:本题考查了简易逻辑的判定、不等式的性质、函数在取得极值的充要条件、函数的轴对称、函数的周期性,考查了推理能力与计算能力,属于中档题.



 全能测控一本好卷系列答案
全能测控一本好卷系列答案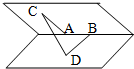 如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2
如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2