
分析 (Ⅰ)求出f'(x)=xex+2ax=x(ex+2a),通过(i)当a>0时,判断函数的单调性,判断零点个数;(ii)若a=0,判断f(x)只有一个零点.(iii)若a<0,利用单调性判断零点个数即可.
(Ⅱ)不妨设x1<x2.推出x1<-x2.利用函数f(x)在(-∞,0)单调递减,证明f(-x2)<0.令g(x)=(-x-1)e-x+(1-x)ex,x∈(0,+∞).利用g'(x)=-x(e-x+ex)<0,转化证明即可.
解答 (本小题满分12分)
解:(Ⅰ)f'(x)=xex+2ax=x(ex+2a)(1分)
(i)当a>0时,
函数f(x)在(-∞,0)单调递减,在(0,+∞)单调递增. (2分)
∵f(0)=-1<0,f(2)=e2+4a>0,
取实数b满足b<-2且b<lna,则f(b)>a(b-1)+ab2=a(b2+b-1)>a(4-2-1)>0,
(3分)
所以f(x)有两个零点. (4分)
(ii)若a=0,则f(x)=(x-1)ex,故f(x)只有一个零点. (5分)
(iii)若a<0,由(I)知,
当$a≥-\frac{1}{2}$,则f(x)在(0,+∞)单调递增,又当x≤0时,f(x)<0,故f(x)不存在两个零点;
当$a<-\frac{1}{2}$,则函数在(ln(-2a),+∞)单调递增;在(0,ln(-2a))单调递减.又当x≤1时,f(x)<0,故不存在两个零点. (6分)
综上所述,a的取值范围是(0,+∞). (7分)
证明:(Ⅱ)不妨设x1<x2.
由(Ⅰ)知x1∈(-∞,0),x2∈(0,+∞),-x2∈(-∞,0),则x1+x2<0等价于x1<-x2.
因为函数f(x)在(-∞,0)单调递减,
所以x1<-x2等价于f(x1)>f(-x2),即证明f(-x2)<0.(8分)
由$f({x_2})=({{x_2}-1}){e^{x_2}}+ax_2^2=0$,得$ax_2^2=({1-{x_2}}){e^{x_2}}$,$f({-{x_2}})=({-{x_2}-1}){e^{-{x_2}}}+ax_2^2=({-{x_2}-1}){e^{-{x_2}}}+({1-{x_2}}){e^{x_2}}$,(9分)
令g(x)=(-x-1)e-x+(1-x)ex,x∈(0,+∞).(10分)
g'(x)=-x(e-x+ex)<0,g(x)在(0,+∞)单调递减,又g(0)=0,所以g(x)<0,
所以f(-x2)<0,即原命题成立.(12分)
点评 本题考查函数的极值,函数的单调性以及函数的零点个数的问题,考查分类讨论思想以及转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 奖品 缴费(无/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{14}{3}$ | C. | $\frac{26}{3}$ | D. | $\frac{38}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
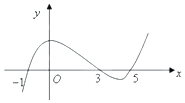
| A. | (-1,3)为函数y=f(x)的递增区间 | B. | (3,5)为函数y=f(x)的递减区间 | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com