
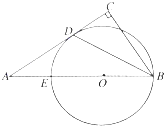
 如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=
如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=| 3 |
| 1 |
| 2 |
| 3 |
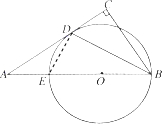 解:连接DE,则∠BDE=∠C=90°,
解:连接DE,则∠BDE=∠C=90°,| 1 |
| 2 |
| 3 |
| 3 |
| BD |
| cos30° |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| π |
| 2 |
| A、y=tanx |
| B、y=|sinx| |
| C、y=cosx |
| D、y=|cosx| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、x0>c |
| B、x0<c |
| C、x0>a |
| D、x0<a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a-c |
| b-c |
| sinB |
| sinA+sinC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在某次试验中,有两个试验数据x,y统计的结果如下面的表格1.
在某次试验中,有两个试验数据x,y统计的结果如下面的表格1.| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
| 序号 | x | y | x2 | xy |
| 1 | 1 | 2 | 1 | 2 |
| 2 | 2 | 3 | 4 | 6 |
| 3 | 3 | 4 | 9 | 12 |
| 4 | 4 | 4 | 16 | 16 |
| 5 | 5 | 5 | 25 | 25 |
| ∑ |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
 |
| y |
 |
| b |
 |
| a |
 |
| a |
 |
| b |
 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| an-2 |
| Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com