
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
分析 利用根的判别式△=b2-4ac=0求得b2+c2-a2=bc,利用余弦定理即可求得cosA的值,结合A的范围即可得解A的值.
解答 解:∵(a2+bc)x2+2$\sqrt{{b}^{2}+{c}^{2}}$x+1=0有两个相等的实数根,
∴△=4(b2+c2)-4(a2+bc)=0,整理可得:b2+c2-a2=bc,
∴由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,
∵A∈(0,180°),
∴A=60°.
故选:C.
点评 本题考查了根的判别式、勾股定理的逆定理,余弦定理在解三角形中的应用,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,属于基础题.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (0,1)∪(1,2) | C. | (0,1)∪(1,2] | D. | (2,+∞)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x≤-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
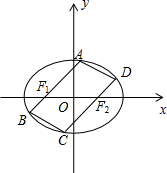 如图,已知椭圆Г:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点分别为F1,F2,过点F1,F2分别作两条平行直线AB,CD交椭圆Г于点A、B、C、D.
如图,已知椭圆Г:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点分别为F1,F2,过点F1,F2分别作两条平行直线AB,CD交椭圆Г于点A、B、C、D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com