
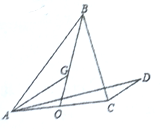
分析 根据题意得出G是△ABC的重心,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出向量$\overrightarrow{AG}$,用$\overrightarrow{AG}$表示出$\overrightarrow{CD}$,写出$\overrightarrow{AD}$的表达式,利用向量相等列出方程组求出λ的值.
解答 解:由已知得G是△ABC的重心,因此$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
由于$\overrightarrow{CD}$∥$\overrightarrow{AG}$,因此设$\overrightarrow{CD}$=k$\overrightarrow{AG}$,
所以$\overrightarrow{CD}$=$\frac{k}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
那么$\overrightarrow{AD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$=$\frac{k}{3}$$\overrightarrow{AB}$+($\frac{k}{3}$+1)$\overrightarrow{AC}$,
$\overrightarrow{AD}$=$\frac{1}{5}$$\overrightarrow{AB}$+λ$\overrightarrow{AC}$,
所以$\left\{\begin{array}{l}{\frac{k}{3}=\frac{1}{5}}\\{\frac{k}{3}+1=λ}\end{array}\right.$,
解得λ=$\frac{6}{5}$.
故答案为:$\frac{6}{5}$.
点评 本题考查了向量在几何中的应用问题,也考查平面向量的基本定理,是基础题目.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
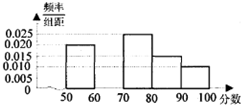
| 组数 | 体能成绩分组 | 爱好数学的人数 | 占本组的频率 |
| 第一组 | [50,60) | 100 | 0.5 |
| 第二组 | [60,70) | 195 | p |
| 第三组 | [70,80) | 120 | 0.6 |
| 第四组 | [80,90) | a | 0.4 |
| 第五组 | [90,100] | 30 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
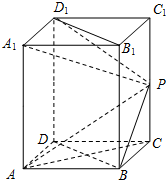 如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e) | B. | (e,+∞) | C. | (0,e+1) | D. | (e+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
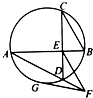 如图,E是圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.
如图,E是圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com