Question

8．某校高一年级学生身体素质能测试的成绩（百分制）分布在[40，100]内，同时为了解学生爱好数学的情况，从中随机抽取了n名学生，这n名学生体能测试成绩的频率分布直方图如图所示，各分数段的“爱好数学”的人数情况如表所示．

组数	体能成绩分组	爱好数学的人数	占本组的频率
第一组	[50，60）	100	0.5
第二组	[60，70）	195	p
第三组	[70，80）	120	0.6
第四组	[80，90）	a	0.4
第五组	[90，100]	30	0.3

（1）求n、p的值；
（2）用分层抽样的方法，从体能成绩在[70，90）的“爱好数学”学生中随机抽取6人参加某项活动，现从6人中随机选取2人担任领队，求两名领队中恰有1人体能成绩在[80，90）的概率．

Answer 1

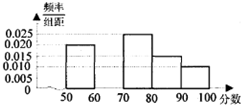
分析 （1）由题知第一组的频率为0.02×10=0.2、人数为$\frac{100}{0.5}$=200，故n=1000．利用第二组的频率为1-（0.02+0.025+0.015+0.01）×10=0.3，求出p；
（2）先计算抽出的6人中有4人体能成绩在[70，80），2人体能成绩在[80，90）．求出所有的情况数与符合条件的情况数，计算出概率．

解答 解：（1）由题知第一组的频率为0.02×10=0.2、人数为$\frac{100}{0.5}$=200，故n=1000．
第二组的频率为1-（0.02+0.025+0.015+0.01）×10=0.3
∴p=$\frac{195}{1000×0.3}$=0.65．…（6分）
（2）由题a=60，
∴抽出的6人中有4人体能成绩在[70，80），2人体能成绩在[80，90）．
从6人中抽取2人有：${C}_{6}^{2}$=15种结果，其中恰有1人在[80，90）的情况有4×2=8种结果，
故所求概率为$\frac{8}{15}$．…（12分）

点评 本题考查等可能事件的概率以及频率分布表，解题的关键是理解概率问题中事件中包含的基本事件的个数和求法，以及能利用频率分布表的特征计算各组的频率与频数，本题是基本知识基础方法考查题，考查了方程的思想