
分析 (1)由求导公式求出函数f(x)的导数,由导数的几何意义和条件列出方程,求出a的值,再确定函数的单调性,即可求函数f(x)的极值;
(2)令$\frac{{x}_{2}}{{x}_{1}}$=t(t>1),即证1-$\frac{1}{t}$<lnt<t-1(t>1).
解答 (1)解:依题意f(x)=lnx+ax,则f′(x)=$\frac{1}{x}$+a
由函数f(x)的图象在点(1,f(1))处的切线平行于x轴得:f′(1)=1+a=0
∴a=-1 …(2分)
所以 f′(x)=$\frac{1}{x}$-1.
因为函数f(x)的定义域为(0,+∞)
由f′(x)>0得0<x<1,由f′(x)<0得x>1,即函数f(x)在(0,1)上单调递增,在(1,+∞)单调递减
所以f(x)极大值=f(1)=-1,没有极小值 …(5分)
(2)证明:依题意得k=$\frac{ln{x}_{2}-ln{x}_{1}-{x}_{2}+{x}_{1}}{{x}_{2}-{x}_{1}}$,
证$\frac{1-{x}_{2}}{{x}_{2}}$<k<$\frac{1-{x}_{1}}{{x}_{1}}$,即证$\frac{1}{{x}_{2}}$<$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$<$\frac{1}{{x}_{1}}$
因x2-x1>0,即证$\frac{{x}_{2}-{x}_{1}}{{x}_{2}}$<ln$\frac{{x}_{2}}{{x}_{1}}$<$\frac{{x}_{2}-{x}_{1}}{{x}_{1}}$
令$\frac{{x}_{2}}{{x}_{1}}$=t(t>1),即证1-$\frac{1}{t}$<lnt<t-1(t>1)…(8分)
令h(t)=lnt+$\frac{1}{t}$-1(t>1)则h′(t)=$\frac{t-1}{{t}^{2}}$>0
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即lnt>1-$\frac{1}{t}$(t>1)①
同理可证:lnt<t-1②
综①②得1-$\frac{1}{t}$<lnt<t-1(t>1),…(11分)
所以$\frac{1-{x}_{2}}{{x}_{2}}$<k<$\frac{1-{x}_{1}}{{x}_{1}}$…(12分)
点评 本题考查导数知识的综合运用,考查不等式的证明.导数的几何意义:过曲线上某点的切线的斜率,就是函数在该点处的导数值.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,-1)∪(1,2) | C. | (-1,3) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
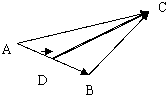 具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
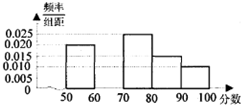
| 组数 | 体能成绩分组 | 爱好数学的人数 | 占本组的频率 |
| 第一组 | [50,60) | 100 | 0.5 |
| 第二组 | [60,70) | 195 | p |
| 第三组 | [70,80) | 120 | 0.6 |
| 第四组 | [80,90) | a | 0.4 |
| 第五组 | [90,100] | 30 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 姓名/成绩 | 1 | 2 | 3 | 4 | 5 | 6 |
| 甲 | 125 | 110 | 86 | 83 | 132 | 92 |
| 乙 | 108 | 116 | 89 | 123 | 126 | 113 |
| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,甲比乙成绩稳定 | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,乙比甲成绩稳定 | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,甲比乙成绩稳定 | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com