
分析 (1)a=0,化简函数的解析式,求出函数的导数,通过令f'(x)=0,求出极值点,判断单调性,然后求解即可;
(2)得到关于x1,x2的方程组,解得x1,x2,求出x1+x2=$\frac{\frac{3}{2}(t+1)lnt}{t-1}$,令h(x)=$\frac{(x+1)lnx}{x-1}$,x∈(1,+∞),求出导函数,然后再构造函数,求出导数判断导函数的符号,推出函数的单调性即可.
解答 解:(1)当a=0时,f(x)=-$\frac{{x}^{2}}{{e}^{x}}$(x>0),f′(x)=$\frac{x(x-2)}{{e}^{x}}$,
令f'(x)=0,则x=2…(2分)
则x∈(0,2),f'(x)<0,y=f(x)单调递减x∈(2,+∞),f'(x)>0,y=f(x)单调递增
所以x=2是函数的一个极小值点,无极大值点.…(4分)
证明:(2)令f(x)=a$\sqrt{x}$-$\frac{{x}^{2}}{{e}^{x}}$=0,则${x}^{\frac{3}{2}}$=aex,
因为函数有两个零点x1,x2(x1<x2)
所以${{x}_{1}}^{\frac{3}{2}}$=a${e}^{{x}_{1}}$,${{x}_{2}}^{\frac{3}{2}}$=a${e}^{{x}_{2}}$,可得$\frac{3}{2}$lnx1=lna+x1,$\frac{3}{2}$lnx2=lna+x2.
故x2-x1=$\frac{3}{2}$(lnx2-lnx1)=$\frac{3}{2}$ln$\frac{{x}_{2}}{{x}_{1}}$.…(6分)
设$\frac{{x}_{2}}{{x}_{1}}$=t,则t>1,且 $\left\{\begin{array}{l}{{x}_{2}={tx}_{1}}\\{{x}_{2}{-x}_{1}=\frac{3}{2}lnt}\end{array}\right.$,
解得x1=$\frac{\frac{3}{2}lnt}{t-1}$,x2=$\frac{\frac{3}{2}tlnt}{t-1}$.
所以:x1+x2=$\frac{\frac{3}{2}(t+1)lnt}{t-1}$.①…(8分)
令h(x)=$\frac{(x+1)lnx}{x-1}$,x∈(1,+∞),
则h′(x)=$\frac{-2lnx+x-\frac{1}{x}}{{(x-1)}^{2}}$.…(10分)
令u(x)=-2lnx+x-$\frac{1}{x}$,得u′(x)=($\frac{x-1}{x}$)2.
当x∈(1,+∞)时,u'(x)>0.因此,u(x)在(1,+∞)上单调递增,
故对于任意的x∈(1,+∞),u(x)>u(1)=0,
由此可得h'(x)>0,故h(x)在(1,+∞)上单调递增.
因此,由①可得x1+x2随着t的增大而增大.…(12分).
点评 本题考查函数的导数的综合应用,构造法的应用,导函数的符号的判断,最值的求法,考查计算能力分析问题解决问题的能力.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
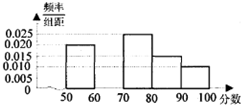
| 组数 | 体能成绩分组 | 爱好数学的人数 | 占本组的频率 |
| 第一组 | [50,60) | 100 | 0.5 |
| 第二组 | [60,70) | 195 | p |
| 第三组 | [70,80) | 120 | 0.6 |
| 第四组 | [80,90) | a | 0.4 |
| 第五组 | [90,100] | 30 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e) | B. | (e,+∞) | C. | (0,e+1) | D. | (e+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
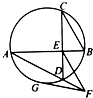 如图,E是圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.
如图,E是圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com