
分析 由f(0)=-2,f(-1)=1直接求出b和c的值,然后写出g(x)的解析式,在两段中分别令函数值为0,解方程即可.
解答 解:由已知当x≤0时f(x)=-x2+bx+c,
由待定系数得:$\left\{\begin{array}{l}{f(0)=c=-2}\\{f(-1)=-1-b+c=1}\end{array}\right.$解得c=-2,b=-4;
故f(x)=$\left\{\begin{array}{l}{x=-2,x>0}\\{-{x}^{2}-4x-2,x≤0}\end{array}\right.$,令f(x)+x=0,
分别解之得x1=2,x2=-1,x3=-2,即函数共有3个零点.
故答案为:3.
点评 本题考查待定系数法求分段函数的解析式、零点,属基本运算的考查.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 体能成绩分组 | 爱好数学的人数 | 占本组的频率 |
| 第一组 | [50,60) | 100 | 0.5 |
| 第二组 | [60,70) | 195 | p |
| 第三组 | [70,80) | 120 | 0.6 |
| 第四组 | [80,90) | a | 0.4 |
| 第五组 | [90,100] | 30 | 0.3 |
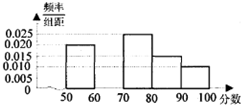
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C是B的真子集、B是A的真子集 | B. | A是B的真子集、B是C的真子集 | ||
| C. | C是A的真子集、A=B | D. | A=B=C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
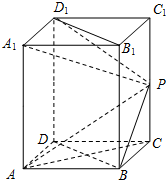 如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com