
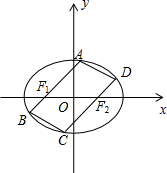
 如图,已知椭圆Г:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点分别为F1,F2,过点F1,F2分别作两条平行直线AB,CD交椭圆Г于点A、B、C、D.
如图,已知椭圆Г:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点分别为F1,F2,过点F1,F2分别作两条平行直线AB,CD交椭圆Г于点A、B、C、D.分析 (I)设AB方程为x=my-1,则CD方程为x=my+1,分别与椭圆方程联立得出A,B,C,D坐标的关系,利用弦长公式即可得出|AB|=|CD|;
(II)求出S△AOB的面积的最大值,即可得出四边形ABCD面积的最大值.
解答 解:(I)F1(-1,0),F2(1,0),
设A(x1,y1),B(x2,y2),直线AB的方程为x=my-1.
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{x=my-1}\end{array}\right.$,消元得(3m2+4)y2-6my-9=0,
∴y1+y2=$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$.
设C(x3,y3),D(x4,y4),直线CD的方程为x=my+1.
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{x=my+1}\end{array}\right.$,消元得(3m2+4)y2+6my-9=0.
∴y3+y4=-$\frac{6m}{3{m}^{2}+4}$,y3y4=-$\frac{9}{3{m}^{2}+4}$.
∴y1+y2=-(y3+y4),y1y2=y3y4,
∴|y1-y2|=|y3-y4|,
∵|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|,|CD|=$\sqrt{1+{m}^{2}}$|y3-y4|,
∴|AB|=|CD|.
(II)∵四边形ABCD是平行四边形,
∴S?ABCD=4S△AOB,
又S△AOB=$\frac{1}{2}$|OF1||y1-y2|=$\frac{1}{2}$$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}$$\sqrt{(\frac{6m}{3{m}^{2}+4})^{2}+\frac{36}{3{m}^{2}+4}}$=6$\sqrt{\frac{{m}^{2}+1}{(3{m}^{2}+4)^{2}}}$=6$\sqrt{\frac{1}{9({m}^{2}+1)+\frac{1}{{m}^{2}+1}+6}}$.
设m2+1=t,f(t)=9t+$\frac{1}{t}$,则t≥1,f′(t)=9-$\frac{1}{{t}^{2}}$>0,
∴f(t)在[1,+∞)上为增函数,∴f(t)≥f(1)=10.
∴S△AOB≤6$\sqrt{\frac{1}{16}}$=$\frac{3}{2}$,
∴四边形ABCD面积的最大值为4×$\frac{3}{2}$=6.
点评 本题考查了直线与椭圆的位置关系,函数最值的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | C是B的真子集、B是A的真子集 | B. | A是B的真子集、B是C的真子集 | ||
| C. | C是A的真子集、A=B | D. | A=B=C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
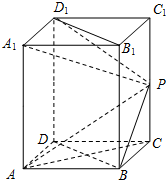 如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{π}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com