
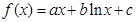 (
(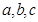 是常数)在
是常数)在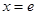 处的切线方程为
处的切线方程为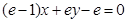 ,且
,且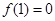 .
.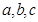 的值;
的值;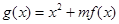 (
(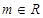 )在区间
)在区间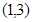 内不是单调函数,求实数
内不是单调函数,求实数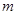 的取值范围;
的取值范围;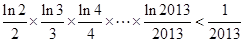 .
.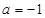 ,
,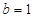 ,
,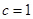 ;(Ⅱ)实数
;(Ⅱ)实数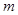 的取值范围是
的取值范围是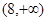 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.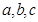 的值,由函数
的值,由函数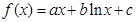 (
(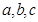 是常数)在
是常数)在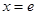 处的切线方程为
处的切线方程为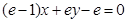 ,只需对
,只需对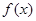 求导,让它的导数在
求导,让它的导数在 处的值即为切线的斜率,这样能得到
处的值即为切线的斜率,这样能得到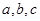 的一个关系式,由
的一个关系式,由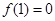 ,代入函数中,又得到
,代入函数中,又得到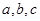 的一个关系式,因为三个参数,需再找一个关系式,,注意到
的一个关系式,因为三个参数,需再找一个关系式,,注意到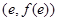 在切线上,可代入切线方程得到
在切线上,可代入切线方程得到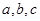 的一个关系式,三式联立方程组即可,解此类题,关键是找
的一个关系式,三式联立方程组即可,解此类题,关键是找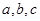 的关系式,有几个参数,需找几个关系式;(Ⅱ)若函数
的关系式,有几个参数,需找几个关系式;(Ⅱ)若函数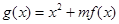 (
(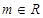 )在区间
)在区间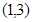 内不是单调函数,即它的导函数在区间
内不是单调函数,即它的导函数在区间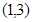 内不恒正或恒负,即
内不恒正或恒负,即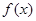 在区间
在区间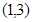 内有极值点,而
内有极值点,而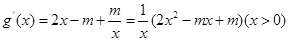 ,只要
,只要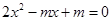 在区间
在区间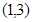 内有解,从而转化为二次函数根的分布问题,分两种情况:在区间
内有解,从而转化为二次函数根的分布问题,分两种情况:在区间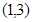 内有一解,在区间
内有一解,在区间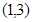 内有两解,结合二次函数图像,从而求出实数
内有两解,结合二次函数图像,从而求出实数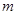 的取值范围;(Ⅲ)证明:
的取值范围;(Ⅲ)证明: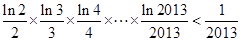 ,注意到
,注意到 ,只需证明
,只需证明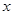 在
在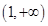 上
上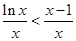 即可,即
即可,即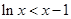 ,而
,而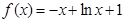 ,只需证明
,只需证明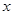 在
在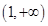 上
上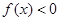 即可,而
即可,而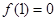 ,即
,即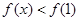 ,只需证
,只需证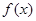 在
在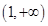 上为减函数,这很容易证出,此题构思巧妙,考查知识点多,学科知识点融合在一起,的确是一个好题,起到把关题作用.
上为减函数,这很容易证出,此题构思巧妙,考查知识点多,学科知识点融合在一起,的确是一个好题,起到把关题作用.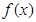 的定义域为
的定义域为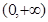 ,
,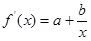 , 因为
, 因为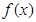 在
在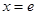 处的切线方程为
处的切线方程为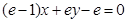 ,所以
,所以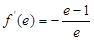 ,且
,且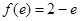 ,即
,即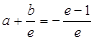 ,且
,且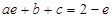 , 又
, 又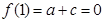 ,解得
,解得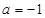 ,
,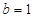 ,
, ,
,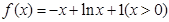 , 因此,
, 因此,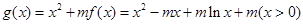 ,
, 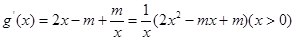 ,令
,令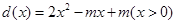 . (ⅰ)当函数
. (ⅰ)当函数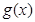 在
在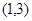 内有一个极值时,
内有一个极值时,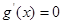 在
在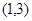 内有且仅有一个根,即
内有且仅有一个根,即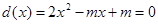 在
在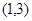 内有且仅有一个根,又因为
内有且仅有一个根,又因为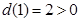 ,当
,当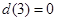 ,即
,即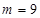 时,
时,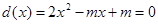 在
在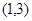 内有且仅有一个根
内有且仅有一个根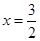 ,当
,当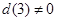 时,应有
时,应有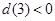 ,即
,即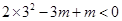 ,解得
,解得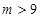 ,所以有
,所以有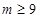 . (ⅱ)当函数
. (ⅱ)当函数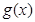 在
在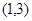 内有两个极值时,
内有两个极值时,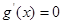 在
在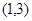 内有两个根,即二次函数
内有两个根,即二次函数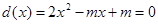 在
在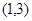 内有两个不等根,所以
内有两个不等根,所以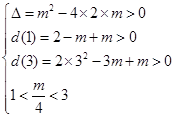 ,解得
,解得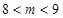 . 综上,实数
. 综上,实数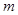 的取值范围是
的取值范围是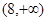 .
. 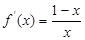 ,所以当
,所以当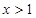 时,有
时,有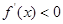 ,所以
,所以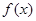 在
在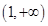 上为减函数,因此当
上为减函数,因此当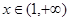 时,
时,  ,即
,即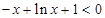 , 即当
, 即当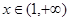 时,
时, 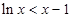 , 所以
, 所以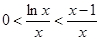 对一切
对一切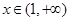 都成立,所以
都成立,所以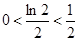 ,
, 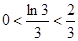 ,
,  , …,
, …, 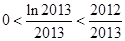 ,所以
,所以 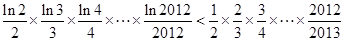 , 所以
, 所以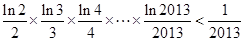 .
. 

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com