
| A. | 命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0” | |
| B. | 实数x>y是x2>y2成立的充要条件 | |
| C. | 设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题 | |
| D. | 命题“若cosα≠1,则α≠0”为真命题 |
分析 写出原命题的否定可判断A;举出反例x=1,y=-1,可判断B;根据复合命题真假判断的真值表,可判断C,利用余弦函数的图象和性质,可判断D.
解答 解:命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1<0”,故A错误;
x=1,y=-1时,x>y成立,但x2>y2不成立,故x>y不是x2>y2成立的充要条件,故B错误;
若“p∨q”为假命题,则p,q均为假命题,¬p,¬q均为真命题,“¬p∧¬q”也为真命题,故C错误;
命题“若cosα≠1,则α≠0”为真命题,故D正确;
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了全称命题,特称命题,复合命题,四种命题,难度中档.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
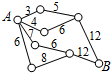 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com