
分析 (1))令|2x+1|=0,解得x=-$\frac{1}{2}$,令|x-2|=0,解得x=2.对x分类讨论即可得出.
(2)令g(x)=f(x)+x,当x≤$-\frac{1}{2}$时,g(x)=|x-a|-x-1,由a$<-\frac{1}{2}$,可得g(x)=$\left\{\begin{array}{l}{-1-a,a<x≤-\frac{1}{2}}\\{-2x+a-1,x≤a}\end{array}\right.$,对于?x∈$(-∞,-\frac{1}{2}]$,使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈$(-∞,-\frac{1}{2}]$,利用图象,即可得出.
解答 解:(1))令|2x+1|=0,解得x=-$\frac{1}{2}$,令|x-2|=0,解得x=2.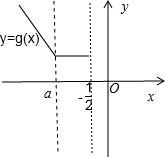
当x≥2时,原不等式化为:2x+1+x-2<4,解得x$<\frac{5}{3}$,此时无解;
当$-\frac{1}{2}$<x<2时,原不等式化为:2x+1+2-x<4,解得x<1,可得$-\frac{1}{2}$<x<1;
当$x≤-\frac{1}{2}$时,原不等式化为:-2x-1+2-x<4,解得x>-1,可得-1<x≤$-\frac{1}{2}$.
综上可得:原不等式的解集为{x|-1<x<1}.
(2)令g(x)=f(x)+x,当x≤$-\frac{1}{2}$时,g(x)=|x-a|-x-1,由a$<-\frac{1}{2}$,
可得g(x)=$\left\{\begin{array}{l}{-1-a,a<x≤-\frac{1}{2}}\\{-2x+a-1,x≤a}\end{array}\right.$,对于?x∈$(-∞,-\frac{1}{2}]$,
使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈$(-∞,-\frac{1}{2}]$,
作出g(x)的图象,可得:[g(x)]min=g(a)=-a-1,
∴-a-1≥3,可得a≤-4.
点评 本题考查了绝对值不等式的解法、不等式的解法、数形结合方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | lg2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
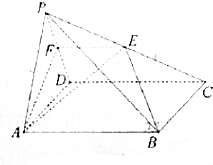 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2<x≤3} | B. | {x|x≥-1} | C. | {x|2≤x<3} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0” | |
| B. | 实数x>y是x2>y2成立的充要条件 | |
| C. | 设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题 | |
| D. | 命题“若cosα≠1,则α≠0”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com