
分析 由(1+2i)•z=|1+2i|,得$z=\frac{|1+2i|}{1+2i}$,再由复数求模公式求出分子,然后利用复数代数形式的乘除运算化简复数z,则z共轭复数可得,则答案可求.
解答 解:由(1+2i)•z=|1+2i|,
得$z=\frac{|1+2i|}{1+2i}$=$\frac{\sqrt{5}}{1+2i}=\frac{\sqrt{5}(1-2i)}{(1+2i)(1-2i)}=\frac{\sqrt{5}-2\sqrt{5}i}{5}$=$\frac{\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}i$,
则z的共轭复数$\overrightarrow{z}$为:$\frac{\sqrt{5}}{5}+\frac{2\sqrt{5}}{5}i$,
其虚部为:$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查了复数代数形式的乘除运算,考查了共轭复数的求法,是基础题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{ED}$=$\frac{\overrightarrow{a}-\overrightarrow{b}}{3}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).
如图,在△ABC中,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{ED}$=$\frac{\overrightarrow{a}-\overrightarrow{b}}{3}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
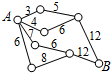 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e=$\sqrt{2}$ | B. | e=$\frac{\sqrt{6}}{2}$ | C. | e=$\frac{\sqrt{30}}{5}$ | D. | e=$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com