
 如图所示,E、F分别是矩形ABCD的边AB、BC上的点(E、F不与边的端点重合).已知线段BF、BC的长分别为m、n、AB、BE的长是关于x的方程x2-18x+mn=0的两个根.
如图所示,E、F分别是矩形ABCD的边AB、BC上的点(E、F不与边的端点重合).已知线段BF、BC的长分别为m、n、AB、BE的长是关于x的方程x2-18x+mn=0的两个根.分析 (1)利用平面几何知识证得△FBE∽△ABC,进一步得到∠BFE=∠BAC,从而得到A、E、F、C四点共圆;
(2)求解方程x2-18x+mn=0的两个根,得到BE=2,AB=16.设所求外接圆的圆心为O,半径为R,则圆心O为线段CE的中垂线与线段BD的中垂线的交点,利用勾股定理求得四边形CBDE外接圆的半径的平方得答案.
解答 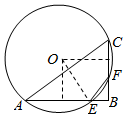 (1)证明:连接EF,根据题意在△BEF和△ACB中,BF•BC=mn=BE•AB,
(1)证明:连接EF,根据题意在△BEF和△ACB中,BF•BC=mn=BE•AB,
即$\frac{BF}{AB}=\frac{BE}{CB}$.…(2分)
又∠FBE=∠CBA,从而△FBE∽△ABC…(4分)
因此∠BFE=∠BAC.
所以A、E、F、C四点共圆.…(5分)
(2)解:当m=4,n=8时,方程x2-18x+mn=0的两个根为x1=2,x2=16.
故BE=2,AB=16…(7分)
如图,设圆心为O,AE,CF的中点分别为Q,H,连接OQ,OH
则OE2=OQ2+EQ2=($\frac{16-2}{2}$)2+(4+$\frac{8-4}{2}$)2=85…(9分)
故四边形AEFC外接圆的面积为85π.…(10分)
点评 本题考查圆内接多边形性质的判断,考查分析问题和求解问题的能力,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
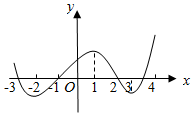 如图y=f(x)的导函数的图象,现有四种说法:
如图y=f(x)的导函数的图象,现有四种说法:| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com