
(本小题满分12分)在等比数列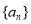 中,已知
中,已知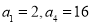 .
.
(Ⅰ)求数列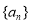 的通项公式.
的通项公式.
(Ⅱ)若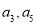 分别为等差数列
分别为等差数列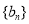 的第3项和第5项,试求数列
的第3项和第5项,试求数列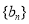 的前
的前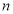 项和
项和 .
.
(1)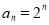 ;(2)
;(2)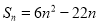 .
.
【解析】
试题分析:(1)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(2)等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前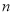 项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
试题解析:(Ⅰ)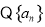 为等比数列
为等比数列
∴ 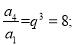
∴ 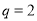
∴ 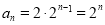 6分
6分
(Ⅱ)∵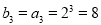 ,
,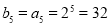 ,又因为
,又因为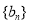 为等差数列
为等差数列
∴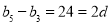
∴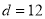
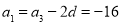
∴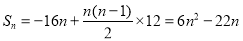 . 12分
. 12分
考点:1、等比数列的通项公式;2、等比数列的前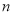 项和公式.
项和公式.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2014-2015学年吉林省长春市高三上学期阶段性考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆: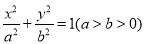 上任意一点到两焦点
上任意一点到两焦点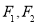 距离之和为
距离之和为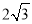 ,离心率为
,离心率为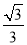 ,动点
,动点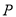 在直线
在直线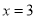 上,过
上,过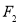 作直线
作直线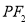 的垂线
的垂线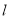 ,设
,设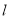 交椭圆于
交椭圆于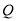 点.
点.
(1)求椭圆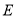 的标准方程;
的标准方程;
(2)证明:直线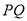 与直线
与直线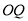 的斜率之积是定值;
的斜率之积是定值;
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
在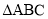 中,角
中,角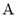 ,
,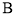 ,
,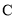 的对边分别为
的对边分别为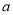 ,
,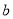 ,
,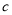 ,且
,且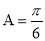 ,
,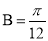 ,
,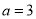 ,则
,则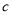 的值为( )
的值为( )
A.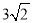 B.
B. C.
C.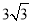 D.
D.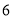
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—1:几何证明选讲
如图,已知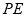 切⊙
切⊙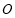 于点
于点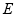 ,割线
,割线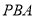 交⊙
交⊙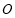 于
于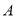 、
、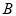 两点,
两点, 的平分线和
的平分线和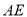 、
、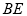 分别交于点
分别交于点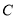 、
、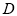 .求证:
.求证:
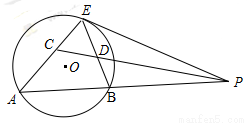
(1)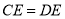 ;
;
(2)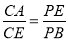 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:选择题
已知定义在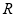 上的可导函数
上的可导函数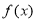 的导函数为
的导函数为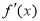 ,若对于任意实数
,若对于任意实数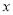 ,有
,有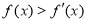 ,且
,且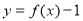 为奇函数,则不等式
为奇函数,则不等式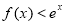 的解集为
的解集为
A.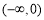 B.
B.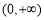 C.
C.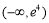 D.
D.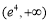
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试理科数学试卷(解析版) 题型:选择题
己知定义在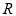 上的可导函数
上的可导函数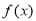 的导函数为
的导函数为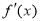 ,满足
,满足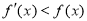 ,且
,且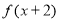 为偶函数,
为偶函数,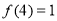 ,则不等式
,则不等式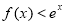 的解集为
的解集为
A.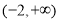 B.
B.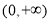
C.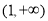 D.
D.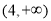
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:解答题
(本题满分12分)己知斜三棱柱 的底面是边长为
的底面是边长为 的正三角形,侧面
的正三角形,侧面 为菱形,
为菱形, ,平面
,平面 平面
平面 ,
, 是
是 的中点.
的中点.

(1)求证:
 ;
;
(2)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com