
分析 (1)由抛物线方程 求得焦点坐标,求得c的值,由双曲线的离心率公式求得其离心率,则e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,即可求得椭圆的半长轴a的值,则b2=a2-c2,即可求得半短轴,即可求得椭圆的方程;
(2)将直线方程代入椭圆方程,由韦达定理求得$-2{x_1}=\frac{{16{k^2}-4}}{{1+4{k^2}}}$,则${x_1}=\frac{{2-8{k^2}}}{{1+4{k^2}}}$,${y_1}=k({{x_1}+2})=\frac{4k}{{1+4{k^2}}}$即可求得B点坐标,由中点坐标公式求得M点坐标,分类当k=0时及当k≠0时,由$\overrightarrow{QA}$•$\overrightarrow{QB}$=4,根据向量的坐标表示,即可求得y0的值.
解答 解:(1)抛物线${y^2}=4\sqrt{3}x$的焦点坐标为$({\sqrt{3},0})$,
所以$c=\sqrt{3}$…(1分)
双曲线$\frac{x^2}{3}-{y^2}=1$的离心率为$\frac{2}{{\sqrt{3}}}$,
所以椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,解得:a=2,
所以b2=1…(3分)
∴椭圆方程为:$\frac{x^2}{4}+{y^2}=1$;…(4分)
(2)由(1)知A(-2,0),且直线l的斜率必存在,设斜率为k,
则直线方程为:y=k(x+2),设点B的坐标为(x1,y1),
联立方程$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=k({x+2})\end{array}\right.$,方程消去y整理得:(1+4k2)x2+16k2x+(16k2-4)=0…(5分)
A,B两点坐标满足上述方程,由韦达定理得$-2{x_1}=\frac{{16{k^2}-4}}{{1+4{k^2}}}$,
所以${x_1}=\frac{{2-8{k^2}}}{{1+4{k^2}}}$,${y_1}=k({{x_1}+2})=\frac{4k}{{1+4{k^2}}}$
所以A(-2,0),B的坐标为$({\frac{{2-8{k^2}}}{{1+4{k^2}}},\frac{4k}{{1+4{k^2}}}})$,…(6分)
线段AB的中点为M,则M点坐标为$({\frac{{-8{k^2}}}{{1+4{k^2}}},\frac{2k}{{1+4{k^2}}}})$…(7分)
以下分两种情况:
①当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,于是$\overrightarrow{QA}=({-2,-{y_0}}),\overrightarrow{QB}=({2,-{y_0}})$,
$\overrightarrow{QA}•\overrightarrow{QB}=-4+y_0^2=4⇒{y_0}=±2\sqrt{2}$…(8分)
②当k≠0时,线段AB的垂直平分线方程为$y-\frac{2k}{{1+4{k^2}}}=-\frac{1}{k}({x+\frac{{8{k^2}}}{{1+4{k^2}}}})$,
令x=0,解得${y_0}=-\frac{6k}{{1+4{k^2}}}$,
由$\overrightarrow{QA}=({-2,-{y_0}}),\overrightarrow{QB}=({{x_1},{y_1}-{y_0}})$…(9分)
∴$\overrightarrow{QA}$•$\overrightarrow{QB}$=-2x1-y0(y1-y0),
=-2×$\frac{2-8{k}^{2}}{1+4{k}^{2}}$+$\frac{6k}{1+4{k}^{2}}$($\frac{4k}{1+4{k}^{2}}$+$\frac{6k}{1+4{k}^{2}}$),
=$\frac{4(16{k}^{4}+15{k}^{2}-1)}{(1+4{k}^{2})^{2}}$=4…(10分)
整理得:$7{k^2}=2⇒k=±\frac{{\sqrt{14}}}{7},{y_0}=±\frac{{2\sqrt{14}}}{5}$…(11分)
综上所述,${y_0}=±2\sqrt{2}$或${y_0}=±\frac{{2\sqrt{14}}}{5}$.…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查双曲线及抛物线的简单性质,考查直线与椭圆的位置关系,韦达定理,中点坐标公式及向量数量积的坐标表示的综合运用,考查计算能力,属于中档题.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{81π}{4}$ | C. | 9π | D. | $\frac{243π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}={({-1})^{n+1}}({2n+1})$ | B. | ${a_n}={({-1})^{n+1}}({2n-1})$ | C. | ${a_n}={({-1})^n}({2n+1})$ | D. | ${a_n}={({-1})^n}({2n-1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{9}{20}$ | C. | $\frac{20}{21}$ | D. | $\frac{10}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
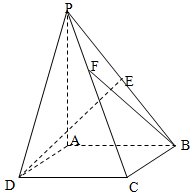 如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,AB=1,PA=2,E为PB的中点,点F在棱PC上,且PF=λPC.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,AB=1,PA=2,E为PB的中点,点F在棱PC上,且PF=λPC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com