
分析 根据f(x)定义域为全体实数,可得mx2-2x+1>0,方程x2+(m-3)x+m=0的一根在(0,1)内,另一根在(1,2)内,利用根的分布建立不等式求解m的范围.要求s∨t为真命题,先求解出s∧t为假命题时,实数m的取值范围,即可得到s∨t为真命题实数m的取值范围.
解答 解:由题意,函数f(x)=ln(mx2-2x+1)的定义域为全体实数;
∴mx2-2x+1>0对一切实数x恒成立,
可得:$\left\{\begin{array}{l}{m>0}\\{△<0}\end{array}\right.$,即$\left\{\begin{array}{l}{m>0}\\{4-4m<0}\end{array}\right.$,
解得:m>1.
令g(x)=x2+(m-3)x+m=0的一根在(0,1)内,另一根在(1,2)内.
可得:$\left\{\begin{array}{l}{g(0)>0}\\{g(1)<0}\\{g(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{m>0}\\{2m<2}\\{3m>2}\end{array}\right.$,
解得:$\frac{2}{3}<m<1$.
当s∧t为假命题时:则s为假,且t也为假.
即$\left\{\begin{array}{l}{m≤1}\\{1≤m或m≤\frac{2}{3}}\end{array}\right.$,
∴得m的范围是(-∞,$\frac{2}{3}$]∪{1}
故得s∨t为真命题,实数m的取值范围为($\frac{2}{3},1$)∪(1,+∞).
点评 本题考查的知识点是二次函数的性质,其中根据方程的根与零点零点的关系,根的分布建立不等式是解答本题的关键.要求s∨t为真命题时m的范围,可以通过求解出s∧t为假命题来解决.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 0 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
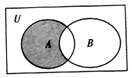 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任何事件的概率总是在(0,1]之间 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 随着试验次数的增加,事件发生的频率一般会稳定于概率 | |
| D. | 概率是随机的,在试验前不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com