
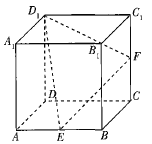
【题目】如图,在棱长为12的正方体![]() 中,已知E,F分别为棱AB,
中,已知E,F分别为棱AB,![]() 的中点,若过点
的中点,若过点![]() ,E,F的平面截正方体
,E,F的平面截正方体![]() 所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面
所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面![]() ,ABCD的交线所成角的余弦值为________.
,ABCD的交线所成角的余弦值为________.
【答案】![]()
![]()
【解析】
延长DC,与![]() 的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的延长线交于点M,连接
的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的延长线交于点M,连接![]() ,交
,交![]() 于点N.连接NE,FH,作出截面多边形,由此易求该截面多边形的周长;多边形与平面
于点N.连接NE,FH,作出截面多边形,由此易求该截面多边形的周长;多边形与平面![]() ,ABCD的交线分别为
,ABCD的交线分别为![]() 与
与![]() ,由面面平行的性质定理得
,由面面平行的性质定理得![]() ∥
∥![]() ,则
,则![]() 为多边形与平面
为多边形与平面![]() ,ABCD的交线所成的角或其补角,利用余弦定理计算
,ABCD的交线所成的角或其补角,利用余弦定理计算![]() 即可.
即可.
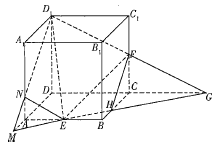
如图,延长DC,与![]() 的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的
的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的
延长线交于点M,连接![]() ,交
,交![]() 于点N.连接NE,FH,
于点N.连接NE,FH,
因为正方体![]() 的棱长为12,
的棱长为12,
所以![]() .
.
因为![]() ∥
∥![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
同理可得![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
易知![]() ,所以
,所以![]() ,
,
又![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,
,
则该多边形的周长为![]() .
.
由面面平行的性质定理得![]() ∥
∥![]() ,
,
则![]() 为多边形与平面
为多边形与平面![]() ,ABCD的交线所成的角或其补角.
,ABCD的交线所成的角或其补角.
因为![]() ,所以
,所以![]() ,
,
所以该多边形与平面![]() ,ABCD的交线所成角的余弦值为
,ABCD的交线所成角的余弦值为![]() .
.
故答案为:![]() ;
;![]()


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,设直线
,设直线![]() 过椭圆
过椭圆![]() 的上顶点和右焦点,坐标原点
的上顶点和右焦点,坐标原点![]() 到直线
到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 且斜率不为零的直线交椭圆
且斜率不为零的直线交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之积为非零的常数?若存在,求出定点
的斜率之积为非零的常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件![]() ,“箱中有
,“箱中有![]() 件非优质产品”为事件
件非优质产品”为事件![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)随机查看该品牌粉笔某一箱中的四盒,设![]() 为非优质产品的盒数,求
为非优质产品的盒数,求![]() 的分布列及期望;
的分布列及期望;
(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉笔都是优质产品的箱数的期望比随机购买的箱中每盒粉笔都是优质产品的箱数的期望大10,则所设计的方案有效.讨论该方案是否有效.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1
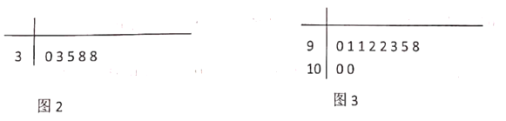
(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,一动圆在
,一动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,此动圆的圆心轨迹为曲线
相外切,此动圆的圆心轨迹为曲线![]() ,椭圆
,椭圆![]() 与曲线
与曲线![]() 有相同的焦点.
有相同的焦点.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与椭圆
与椭圆![]() 相交于第一象限点
相交于第一象限点![]() ,且
,且![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(3)在(2)的条件下,如果椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:四边形
两点,证明:四边形![]() 的对角线的交点是椭圆
的对角线的交点是椭圆![]() 的右顶点.
的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
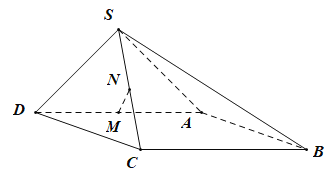
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,
中,底面ABCD为矩形,![]() ,
,![]() ,侧面SAD是以AD为斜边的等腰直角三角形,且平面
,侧面SAD是以AD为斜边的等腰直角三角形,且平面![]() 平面ABCD,M,N分别为AD,SC的中点.
平面ABCD,M,N分别为AD,SC的中点.
(1)求证:![]() 平面SAB.
平面SAB.
(2)求直线BN与平面SAB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com