练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

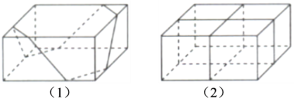
    【题目】春节期间，佳怡准备去探望奶奶，她到商店买了一盒点心.为了美观起见，售货员对点心盒做了一个捆扎（如图（1）所示），并在角上配了一个花结.售货员说，这样的捆扎不仅漂亮，而且比一般的十字捆扎（如图（2）所示）包装更节省彩绳.你同意这种说法吗？请给出你的理由.（注；长方体点心盒的高小于长、宽.）

    【答案】同意，详见解析

    【解析】

    设长方体点心盒子的长、宽、高分别为x，y，z，分别计算两种捆扎方式的彩绳的长度，通过比较，即可得到答案.

    设长方体点心盒子的长、宽、高分别为x，y，z，

    依据是图（2）的捆扎方式，把彩绳的长度记作l，因为长方体的每个面上的那一段绳都与相交的棱垂直，故.

    依据题图（1）的捆扎方式，绳长记作m.示意图如图，由三角形中两边之和大于第三边，得

    ，，，，

    ，，，

    ∴，即，即，

    因此，如题图（1）所示的捆扎方式节省材料.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】曲线y＝1＋与直线y＝k(x－2)＋4有两个交点，则实数k的取值范围是( )

    A. (，＋∞)B. (，]C. (0，)D. (，]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·江苏高考)如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.

    求证：(1)EF∥平面ABC；

    (2)AD⊥AC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）如图所示的某种容器的体积为，它是由圆锥和圆柱两部分连接而成，圆柱与圆锥的底面半径都为．圆锥的高为，母线与底面所成的角为；圆柱的高为，已知圆柱底面的造价为元，圆柱侧面造价为元，圆锥侧面造价为元．

    （1）将圆柱的高表示为底面半径的函数，并求出定义域；

    （2）当容器造价最低时，圆柱的底面半径为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点为极点，轴的非负半轴为极轴建立极坐标系.已知曲线的极坐标方程为，为曲线上的动点，与轴、轴的正半轴分别交于，两点.

    （1）求线段中点的轨迹的参数方程；

    （2）若是（1）中点的轨迹上的动点，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司一年需购买某种原料400吨，设公司每次都购买吨，每次运费为4万元，一年的总存储费用为万元.

    （1）要使一年的总运费与总存储费用之和最小，则每次购买多少吨？

    （2）要使一年的总运费与总存储费用之和不超过200万元，则每次购买量在什么范围？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点为抛物线外一点，过点作抛物线的两条切线，，切点分别为，．

    （Ⅰ）若点为，求直线的方程；

    （Ⅱ）若点为圆上的点，记两切线，的斜率分别为，，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，选项正确的是（ ）

    A. 在回归直线中，变量时，变量的值一定是15

    B. 两个变量相关性越强，则相关系数就越接近于1

    C. 在残差图中，残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适，与带状区域的宽度无关

    D. 若某商品的销售量（件）与销售价格（元/件）存在线性回归方程为，当销售价格为10元时，销售量为100件左右

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的奇函数和偶函数满足：，下列结论正确的有（ ）

    A.，且

    B.，总有

    C.，总有

    D.，使得

    查看答案和解析>>

    同步练习册答案