
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 与
与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() ,
,![]() 两点.
两点.
(1)求线段![]() 中点
中点![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)若![]() 是(1)中点
是(1)中点![]() 的轨迹上的动点,求
的轨迹上的动点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分两层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2:
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 | x | 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
(1)求x,y的值;
(2)在答题纸上完成频率分布直方图;并根据频率分布直方图,估计该工厂B类工人生产能力的平均数(同一组中的数据用该区间的中点值作代表)和中位数.(结果均保留一位小数)


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | 10 | 10 |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值
元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为
元的奖品.已知中奖率为![]() ,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为
,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量比去年同期增长
.若今年国庆期间该商场的购物单数量比去年同期增长![]() ,式预测商场今年国庆期间采办奖品的开销.
,式预测商场今年国庆期间采办奖品的开销.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:

(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
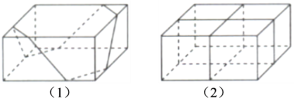
【题目】春节期间,佳怡准备去探望奶奶,她到商店买了一盒点心.为了美观起见,售货员对点心盒做了一个捆扎(如图(1)所示),并在角上配了一个花结.售货员说,这样的捆扎不仅漂亮,而且比一般的十字捆扎(如图(2)所示)包装更节省彩绳.你同意这种说法吗?请给出你的理由.(注;长方体点心盒的高小于长、宽.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱台![]() 中,上底面边长为4,下底面边长为8,高为5,点
中,上底面边长为4,下底面边长为8,高为5,点![]() 分别在
分别在![]() 上,且
上,且![]() .过点
.过点![]() 的平面
的平面![]() 与此四棱台的下底面会相交,则平面
与此四棱台的下底面会相交,则平面![]() 与四棱台的面的交线所围成图形的面积的最大值为
与四棱台的面的交线所围成图形的面积的最大值为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com