练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．甲乙丙三人一起参加机动车驾驶证科目考三试后，与丁相聚，丁询问甲乙丙的考试结果，甲说：“我通过了．”，乙说：“我和甲都通过了．”，丙说：“我和乙都通过了．”甲乙丙三人有且只有一个人说的内容与考试结果不完全相同，甲乙丙中没有通过的是丙．

    分析 分别假设甲和乙的说法考试结果不完全相同，得到矛盾，故可得丙的说法与考试结果不完全相同，再根据甲乙所说判断即可

    解答 解：假设甲说的内容与考试结果不完全相同，则甲没有通过，则乙的说法考试结果不完全相同，故甲说的是正确的，
    假设乙说的内容与考试结果不完全相同，则甲和乙最多有1人通过，根据丙所说可知乙丙通过了，于是可得甲没有通过，则与甲的说法相矛盾，则乙的说法是正确，
    故丙的说法与考试结果不完全相同，于是可得丙没有通过，
    故答案为：丙．

    点评 本题主要考查简单的合情推理，要抓住关键，逐步推断，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．若复数z=$\frac{2}{1+i}$+（1-i）2，则|z|等于（　　）
    A．$\sqrt{10}$B．$\sqrt{2}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列能正确反映《必修1》中指数幂的推广过程的是（　　）
    A．整数指数幂→有理数指数幂→无理数指数幂
    B．有理数指数幂→整数指数幂→无理数指数幂
    C．整数指数幂→无理数指数幂→有理数指数幂
    D．无理数指数幂→有理数指数幂→整数指数幂

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ，|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=1，$\overrightarrow{OP}$=t$\overrightarrow{OA}$，$\overrightarrow{OQ}$=（1-t）$\overrightarrow{OB}$，|$\overrightarrow{PQ}$|在t0时取最小值，当0＜t0＜$\frac{1}{4}$时，cosθ的取值范围为（　　）
    A．（-$\frac{1}{2}$，0）B．（-$\frac{1}{2}$，-$\frac{1}{4}$）C．（$\frac{1}{4}$，1）D．（-$\frac{1}{2}$，$\frac{1}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

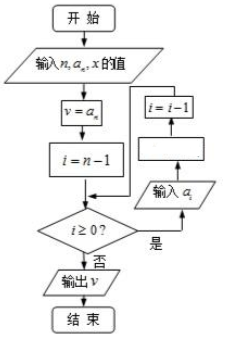    1．我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an-1）x+an-2）x+…+a1）x+a0，首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（　　）
    A．v=vx+aiB．v=v（x+ai）C．v=aix+vD．v=ai（x+v）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．有如图所示的程序框图，则该程序框图表示的算法的功能是（　　）
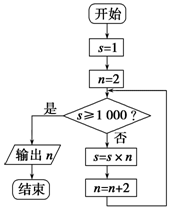
    A．输出使1×2×4×…×n≥1 000成立的最大整数n+2
    B．输出使1×2×4×…×n≥1 000成立的最小整数n+2
    C．输出使1×2×4×…×n≥1 000成立的最小整数n
    D．输出使1×2×4×…×n≥1 000成立的最大整数n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．某几何体的三视图如图所示，则其体积为（　　）
    A．80B．160C．240D．480

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知i是虚数单位，则$\frac{1+i}{1-i}$=（　　）
    A．1B．-1C．iD．-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设f（x）是定义在R上的偶函数，且在（-∞，0]上是增函数，设$a=f（{log_4}7），b=f（{log_{\frac{1}{2}}}3），c=f（{2^{\sqrt{2}}}）$，则a，b，c的大小关系是（　　）
    A．c＜a＜bB．c＜b＜aC．b＜c＜aD．a＜b＜c

    查看答案和解析>>

    同步练习册答案