
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($\frac{1}{4}$,1) | D. | (-$\frac{1}{2}$,$\frac{1}{4}$) |
分析 由向量的运算求得${\overrightarrow{PQ}}^{2}$=(5+4cosθ)t2+(-2-4cosθ)t+1,由二次函数知,当上式取最小值时,t0=$\frac{1+2cosθ}{5+4cosθ}$,根据0<$\frac{1+2cosθ}{5+4cosθ}$<$\frac{1}{4}$,能求出cosθ的取值范围.
解答 解:由题意得:
$\overrightarrow{OA}•\overrightarrow{OB}$=2×1×cosθ=2cosθ,
$\overrightarrow{PQ}$=$\overrightarrow{OQ}-\overrightarrow{OP}$=(1-t)$\overrightarrow{OB}$-t$\overrightarrow{OA}$,
∴${\overrightarrow{PQ}}^{2}$=(1-t)2•${\overrightarrow{OB}}^{2}$+${t}^{2}•{\overrightarrow{OA}}^{2}$-2t(1-t)•$\overrightarrow{OA}•\overrightarrow{OB}$
=(1-t)2+4t2-4t(1-t)cosθ=(5+4cosθ)t2+(-2-4cosθ)t+1,
由二次函数知,当上式取最小值时,${t}_{0}=\frac{1+2cosθ}{5+4cosθ}$,
∵0<t0<$\frac{1}{4}$,∴0<$\frac{1+2cosθ}{5+4cosθ}$<$\frac{1}{4}$,
解得-$\frac{1}{2}$<cosθ<$\frac{1}{4}$.
∴cosθ的取值范围为(-$\frac{1}{2},\frac{1}{4}$).
故选:D.
点评 本题考查向量数量积与向量的夹角,考查二次函数、三角函数、向量、分式不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、运动与方程思想,考查应用意识、创新意识,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(ln2,\frac{{{e^2}-1}}{2})$ | B. | (ln2,e-1) | C. | [1,e-1) | D. | $[1,\frac{{{e^2}-1}}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4+4$\sqrt{2}$ | B. | 8+4$\sqrt{2}$ | C. | 8+2$\sqrt{3}$ | D. | 8+4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | 2x+y-1=0 | C. | x+2y-2=0 | D. | 2x+y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
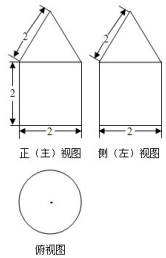 一个几何体的三视图如图所示:
一个几何体的三视图如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com