
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
分析 由偶函数性质得f(x)在[0,+∞)上是减函数,b=f($lo{g}_{\frac{1}{2}}3$)=f(log23),由此利用1<log47<log23=log49<log416=2,${2}^{\sqrt{2}}>{2}^{1}=2$,能判断a,b,c的大小关系.
解答 解:∵f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,
∴f(x)在[0,+∞)上是减函数,
∵$a=f({log_4}7),b=f({log_{\frac{1}{2}}}3),c=f({2^{\sqrt{2}}})$,
1<log47<log23=log49<log416=2,${2}^{\sqrt{2}}>{2}^{1}=2$,
b=f($lo{g}_{\frac{1}{2}}3$)=f(log23),
∴a,b,c的大小关系是c<b<a.
故选:B.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意函数性质的合理运用.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
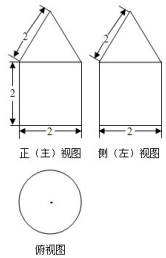 一个几何体的三视图如图所示:
一个几何体的三视图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com