
分析 (1)由题意可得b=2,运用离心率公式和a,b,c的关系,解方程可得a,进而得到所求椭圆方程;
(2)讨论直线CD的斜率不存在,求得圆心到直线的距离,求得弦长AB;直线CD的斜率存在,设CD:y=kx+m,由点到直线的距离公式和联立椭圆方程,消去y,可得x的方程,运用韦达定理和弦长公式,化简整理,结合换元法和二次函数的值域求法,即可得到所求AB的范围.
解答 解:(1)圆${C_2}:{x^2}+{y^2}=4$经过椭圆C1短轴的两个端点,
可得b=2,
离心率为$\frac{{\sqrt{2}}}{2}$,即e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
又c2=a2-b2,
解得c=2,a=2$\sqrt{2}$,
则椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)当$|{CD}|=2\sqrt{3}$时,
圆C2到直线CD的距离为d=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
①当CD⊥x轴时,可将x=±1代入椭圆方程解得y=±$\frac{\sqrt{14}}{2}$,
可得|AB|=$\sqrt{14}$;
②当直线CD的斜率存在时,设CD:y=kx+m,
由d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,可得m2=1+k2,
$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,可得(1+2k2)x2+4kmx+2m2-8=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{2}$•$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{4+8{k}^{2}-{m}^{2}}{(1+2{k}^{2})^{2}}}$
=2$\sqrt{2}$•$\sqrt{\frac{(1+{k}^{2})(3+7{k}^{2})}{(1+2{k}^{2})^{2}}}$,
可令t=1+2k2(t≥1),即k2=$\frac{1}{2}$(t-1),
则|AB|=2$\sqrt{2}$•$\sqrt{\frac{(1+\frac{t-1}{2})(3+\frac{7t-7}{2})}{{t}^{2}}}$
=$\sqrt{2}$•$\sqrt{-\frac{1}{{t}^{2}}+\frac{6}{t}+7}$,
由t≥1,可得0<$\frac{1}{t}$≤1,
-$\frac{1}{{t}^{2}}$+$\frac{6}{t}$+7=-($\frac{1}{t}$-3)2+16∈(7,12],
则$\sqrt{14}$<|AB|≤2$\sqrt{6}$.
综上可得|AB|的取值范围为[$\sqrt{14}$,2$\sqrt{6}$].
点评 本题考查椭圆方程的求法,注意运用离心率公式,考查直线和圆截得的弦长,注意运用勾股定理,以及直线和椭圆方程联立,运用韦达定理和弦长公式,考查换元法及二次函数的值域问题,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
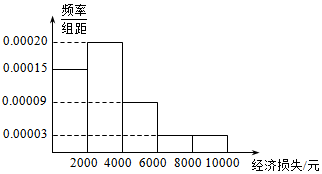 据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
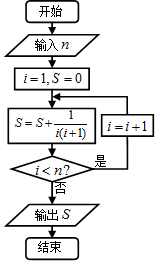
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,-1)∪(-1,0)∪(0,1)∪(1,$\sqrt{2}$) | B. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | ||
| C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | (-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com