
分析 (1)寻找使不等式成立的充分条件,利用同解变形,转化证明42>40.推出结论.
(2)要证的结论与条件之间的联系不明显,直接由条件推出结论的线索不够清晰.于是考虑采用反证法.假设a,b,c不全是正数,这时需要逐个讨论a,b,c不是正数的情形.但注意到条件的特点(任意交换a,b,c的位置不改变命题的条件),我们只要讨论其中一个数(例如a),其他两个数(例如b,c)与这种情形类似.
解答 证明:(1)要证:$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$,只要证 6+7+2$\sqrt{42}$>8+5+4$\sqrt{10}$,
只要证$\sqrt{42}$>2$\sqrt{10}$,即证 42>40. 而 42>40 显然成立,
故原不等式成立.
(2)假设a,b,c不全是正数,即其中至少有一个不是正数.
不妨先设a≤0.下面分a=0和a<0两种情况讨论.
如果a=0,则abc=0,与abc>0矛盾,所以a=0不可能.
如果a<0,那么由abc>0可得
bc<0.
又因为a+b+c>0,所以b+c>-a>0.
于是ab+bc+ca=a(b+c)+bc<0,
这和已知ab+bc+ca>0相矛盾.
因此,a<0也不可能.
综上所述,a>0.
同理可证b>0,c>0.
所以原命题成立.
点评 (1)本题考查用分析法证明不等式,关键是寻找使不等式成立的充分条件.(2)当一个命题的结论是以“至多”“至少”“唯一”或以否定形式出现时,宜用反证法来证.反证法关键是在正确的推理下得出矛盾,矛盾可以是①与已知条件矛盾,②与假设矛盾,③与定义、公理、定理矛盾,④与事实矛盾等方面.反证法常常是解决某些“疑难”问题的有力工具,是数学证明中的一件有力武器.


科目:高中数学 来源: 题型:解答题
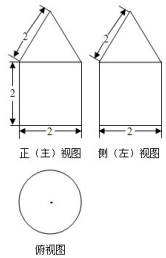 一个几何体的三视图如图所示:
一个几何体的三视图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com