
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可;
(2)求出g(x)的导数,通过讨论a的范围,求出函数的单调区间,结合?x∈(2,+∞),g(x)<0恒成立,确定a的范围即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),---------------------(1分)
当a=$-\frac{1}{2}$时,f(x)=-x2+lnx,$f'(x)=-2x+\frac{1}{x}$=$\frac{{-2{x^2}+1}}{x}$;--------------------(2分)
当$0<x<\frac{{\sqrt{2}}}{2}$,有f'(x)>0;当$x>\frac{{\sqrt{2}}}{2}$,有f'(x)<0,--------------------(3分)
∴f(x)在区间[$\frac{1}{e}$,$\frac{{\sqrt{2}}}{2}$]上是增函数,在[$\frac{{\sqrt{2}}}{2}$,e]上为减函数,--------------------(4分)
又$f(\frac{1}{e})=-1-\frac{1}{e^2}$,f(e)=1-e2,$f(\frac{{\sqrt{2}}}{2})=-\frac{1}{2}-\frac{1}{2}ln2$.,--------------------(5分)
∴fmin(x)=f(e)=1-e2,fmax(x)=$f(\frac{{\sqrt{2}}}{2})=-\frac{1}{2}-\frac{1}{2}ln2$.---------------------(6分)
(2)g(x)=f(x)-2ax=(a-$\frac{1}{2}$)x2+lnx-2ax,则g(x)的定义域为(0,+∞),
g′(x)=$\frac{(x-1)[(2a-1)x-1]}{x}$-----(7分)
①若a>$\frac{1}{2}$,令g'(x)=0,得极值点x1=1,x2=$\frac{1}{2a-1}$,
ⅰ)当2≥x2>x1=1,即$\frac{3}{4}≤a<1$时,在(2,+∞)上有g'(x)>0,
此时g(x)在区间(2,+∞)上是增函数,
并且在该区间上有g(x)∈(g(2),+∞),不合题意;
ⅱ)当x2>2,即$\frac{1}{2}<a<\frac{3}{4}$时,在(2,x2)上g'(x)<0;在(x2,+∞)上g'(x)>0;
所以在(2,+∞)上g(x)先减后增,有g(x)∈[g(x2),+∞),也不合题意;
ⅲ)当x2≤x1=1,即a≥1时,同理可知,g(x)在区间(2,+∞)上是增函数,
有g(x)∈(g(2),+∞),也不合题意;---------------------(10分)
②若a≤$\frac{1}{2}$,则有2a-1≤0,此时在区间(2,+∞)上恒有g'(x)<0,
∴g(x)在(2,+∞)上是减函数;要使g(x)<0在此区间上恒成立,
只须满足g(2)=-2+ln2≤0恒成立⇒a∈R,又a≤$\frac{1}{2}$,---------------------(12分)
∴a的范围是$(-∞,\frac{1}{2}]$,---------------------(13分)
综合①②可知,当a∈$(-∞,\frac{1}{2}]$时,对?x∈(2,+∞),g(x)<0恒成立.-------(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
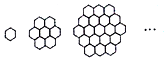 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{16}{3}$ | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,$\frac{3π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$]∪($\frac{5π}{4}$,$\frac{3π}{2}$] | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{5π}{4}$,$\frac{7π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )
如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )| A. | 16π | B. | 8π | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com