
 如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )
如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )| A. | 16π | B. | 8π | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
分析 三视图复原几何体是三棱锥,扩展为长方体设出长方体的三度,利用面积之和,基本不等式求出几何体的外接球的直径,然后求出面积的最小值.
解答 解:三视图复原几何体是三棱锥,
它的外接球的直径就是几何体扩展为长方体的体对角线的长,
长方体的三度为:a,b,c;
所以ab+bc+ac=16,长方体的对角线为$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$≥$\sqrt{ab+bc+ac}$=4,
当且仅当a=b=c时取等号,
所以几何体的外接球的表面积的最小值为:4π•22=16π.
故选A.
点评 本题是基础题,考查三视图复原几何体的图形的判断,几何体的外接球的表面积的求法,基本不等式的应用,注意基本不等式等号成立的前提.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
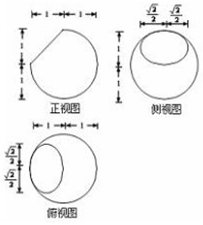 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
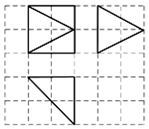 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )| A. | 4+2($\sqrt{2}$+$\sqrt{3}$) | B. | 6+2($\sqrt{2}$+$\sqrt{5}$) | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com