
| A. | ($\frac{π}{4}$,$\frac{3π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$]∪($\frac{5π}{4}$,$\frac{3π}{2}$] | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{5π}{4}$,$\frac{7π}{4}$) |
分析 由题意可得sinx>0,讨论当x=$\frac{π}{2}$时,当0<x<$\frac{π}{2}$时,当$\frac{π}{2}$<x<π时,运用同角的商数关系,结合正切韩寒说的图象,即可得到所求范围.
解答 解:由sin x>|cos x|≥0,
可得sinx>0,
再由x∈(0,2π),
可得x∈(0,π),
当x=$\frac{π}{2}$时,sinx=1,cosx=0,显然成立;
当0<x<$\frac{π}{2}$时,由sinx>cosx,即tanx>1,可得$\frac{π}{4}$<x<$\frac{π}{2}$;
当$\frac{π}{2}$<x<π时,sinx>-cosx,即有$\frac{sinx}{-cosx}$>1,
则tanx<-1,解得$\frac{π}{2}$<x<$\frac{3π}{4}$,
综上可得x∈($\frac{π}{4}$,$\frac{3π}{4}$).
故选:A.
点评 本题考查三角函数的图象和性质,主要考查正切函数的图象,以及分类讨论思想方法,属于中档题.


科目:高中数学 来源: 题型:解答题
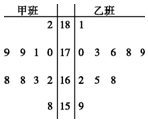 随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示
随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
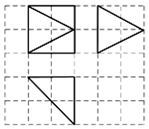 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )| A. | 4+2($\sqrt{2}$+$\sqrt{3}$) | B. | 6+2($\sqrt{2}$+$\sqrt{5}$) | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com