
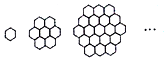
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91. 分析 根据图象的规律可得相邻两项的差的规律可分析得出f(n)-f(n-1)=6(n-1),进而根据合并求和的方法求得f(n)的表达式,问题得以解决.
解答 解:由于f(2)-f(1)=7-1=6,
f(3)-f(2)=19-7=2×6,
f(4)-f(3)=37-19=3×6,
f(5)-f(4)=61-37=4×6,…
因此,当n≥2时,有f(n)-f(n-1)=6(n-1),
所以f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+…+[f(2)-f(1)]+f(1)
=6[(n-1)+(n-2)+…+2+1]+1=3n2-3n+1.
又f(1)=1=3×12-3×1+1,
所以f(n)=3n2-3n+1.
当n=6时,f(6)=3×62-3×6+1=91.
故答案为91.
点评 本题主要考查了数列的问题、归纳推理.属于基础题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
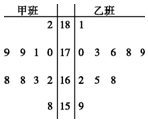 随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示
随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 货币收入x | 40 | 42 | 44 | 47 | 50 |
| 购买商品支出y | 33 | 34 | 36 | 39 | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
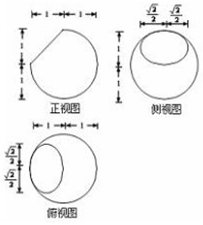 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com