
分析 (Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间,判断函数的极值点的个数即可;
(Ⅱ)分离参数,问题转化为$a≤\frac{{{e^x}+{x^2}-lnx}}{x}$对于?x>0恒成立,设$φ(x)=\frac{{{e^x}+{x^2}-lnx}}{x}(x>0)$,根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)$f'(x)=x+\frac{1}{x}+a$,∵x>0,∴f'(x)∈[a+2,+∞),
①当a+2≥0,即a∈[-2,+∞)时,f'(x)≥0对?x>0恒成立,
f(x)在(0,+∞)单调增,f(x)没有极值点;
②当a+2<0,即a∈(-∞,-2)时,方程x2+ax+1=0有两个不等正数解x1,x2,
$f'(x)=x+\frac{1}{x}+a=\frac{{{x^2}+ax+1}}{x}=\frac{{(x-{x_1})(x-{x_2})}}{x}(x>0)$
不妨设0<x1<x2,则当x∈(0,x1)时,f'(x)>0,f(x)增;
x∈(x1,x2)时,f'(x)<0,f(x)减;x∈(x2,+∞)时,f'(x)>0,f(x)增,
所以x1,x2分别为f(x)极大值点和极小值点,f(x)有两个极值点.
综上所述,当a∈[-2,+∞)时,f(x)没有极值点;
当a∈(-∞,-2)时,f(x)有两个极值点.
(Ⅱ)f(x)≤g(x)?ex-lnx+x2≥ax,由x>0,
即$a≤\frac{{{e^x}+{x^2}-lnx}}{x}$对于?x>0恒成立,
设$φ(x)=\frac{{{e^x}+{x^2}-lnx}}{x}(x>0)$,$φ'(x)=\frac{{({e^x}+2x-\frac{1}{x})x-({e^x}+{x^2}-lnx)}}{x^2}=\frac{{{e^x}(x-1)+lnx+(x+1)(x-1)}}{x^2}$,
∵x>0,∴x∈(0,1)时,φ'(x)<0,φ(x)减,
x∈(1,+∞)时,φ'(x)>0,φ(x)增,
∴φ(x)≥φ(1)=e+1,
∴a≤e+1.
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用以及分类讨论思想,函数恒成立问题,考查转化思想,是一道综合题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
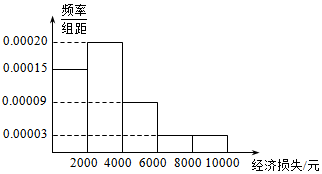 据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
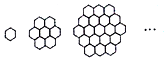 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com