
分析 ${a_1}=\frac{6}{7},{a_n}=\frac{{3{S_n}}}{n+3}({n∈{N_+}})$,即(n+3)an=3Sn,利用递推关系可得:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+2}{n}$.再利用“累乘求积”即可得出.
解答 解:∵${a_1}=\frac{6}{7},{a_n}=\frac{{3{S_n}}}{n+3}({n∈{N_+}})$,∴(n+3)an=3Sn,
n≥2时,(n+2)an-1=3Sn-1,
相减可得:(n+3)an-(n+2)an-1=3an,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+2}{n}$.
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$×$\frac{{a}_{n-1}}{{a}_{n-2}}$×…×$\frac{{a}_{2}}{{a}_{1}}$×a1=$\frac{n+2}{n}$×$\frac{n+1}{n-1}$×$\frac{n}{n-2}$×…×$\frac{6}{4}$×$\frac{5}{3}$×$\frac{4}{2}$×$\frac{6}{7}$=$\frac{(n+2)(n+1)}{7}$.
那么a48=$\frac{50×49}{7}$=350.
故答案为:350.
点评 本题考查了数列递推关系、“累乘求积”,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
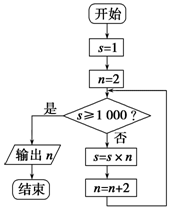
| A. | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B. | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C. | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D. | 输出使1×2×4×…×n≥1 000成立的最大整数n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
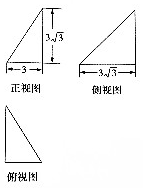 已知某几何体的三视图如图所示,则该几何体的内切球的体积为( )
已知某几何体的三视图如图所示,则该几何体的内切球的体积为( )| A. | $\frac{1}{4}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{1}{2}$π | D. | $\frac{\sqrt{3}}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
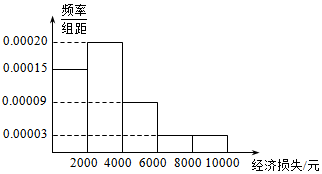 据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com