
分析 可用三角形的两边和大于第三边,及两边差小于第三边,但要注意前者可以取到等号成立,因为可以三点一线.也可用焦半径公式确定a与c的关系.
解答 解:设|PF1|=x,|PF2|=y,则有$\left\{\begin{array}{l}{x=2y}\\{x-y=2a}\end{array}\right.$,
解得x=4a,y=2a,
∵在△PF1F2中,x+y>2c,即4a+2a>2c,4a-2a<2c,
∴1$<\frac{c}{a}$<3,
又因为当三点一线时,4a+2a=2c,
综合得离心率的范围是(1,3],
故答案为(1,3].
点评 本题主要考查了双曲线的简单性质.考查了关于离心率范围的确定.可以在平时的教学过程中总结常见的有关离心率的求法及范围的求法.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
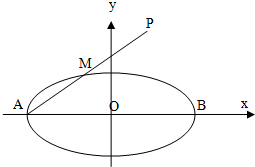 已知椭圆C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右顶点分别为A、B,M为椭圆上的任意一点,A关于M的对称点为P,如图所示,
已知椭圆C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右顶点分别为A、B,M为椭圆上的任意一点,A关于M的对称点为P,如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 吸烟人患肺癌的概率为99% | |
| B. | 认为“吸烟与患肺癌有关”犯错误的概率不超过1% | |
| C. | 吸烟的人一定会患肺癌 | |
| D. | 100个吸烟人大约有99个人患有肺癌 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com