
分析 根据不等式的性质、空间线面位置关系、等比数列定义、三棱锥定义等逐一对各个答案的真假进行判断.
解答  解:对于①,由$\frac{1}{a}$<$\frac{1}{b}$<0得到b<a<0,∴b2>a2,故①是真命题;
解:对于①,由$\frac{1}{a}$<$\frac{1}{b}$<0得到b<a<0,∴b2>a2,故①是真命题;
对于②,若l⊥α,且α⊥β,则l∥β或l?β,故是②假命题;
对于③若-1,a,b,c,-16成等比数列,则a2=-1×b,且b2=-1×(-16),∴b<0,b=-4,故③是真命题;
对于④,如图所示三棱锥C-A1B1C1的四个面可以都是直角三角形.故④是真命题.
故答案是:①③④
点评 此种题型往往比较综合考查多个知识点的概念,处理的关键是熟练掌握各个知识点的概念、定义逐一对各个答案的真假进行判断.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\frac{{\sqrt{3}}}{3}]∪$(1,+∞) | C. | $[\frac{{\sqrt{3}}}{3},1)$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
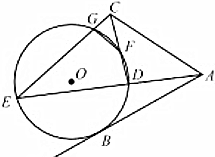 如图,AB是圆O的一条切线,切点为B,直线ABD,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,直线ABD,CFD,CGE都是圆O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com